이번 포스터에서는 활성화 함수(Activation Function)에 대해 얘기해 볼 것이다. 딥러닝 모델을 설계할 때 각 층(Linear, CNN 등)에서 연산이 이루어지고 난 후 출력할 때 주로 활성화 함수를 거친 후에 출력이 된다. 딥러닝에서 필수적으로 사용되는 활성화 함수에 대해 알아보도록 하자.
활성화 함수(Function)
우리 몸에는 신경을 전달하는 뉴런이 있다. 어느 부위에서 자극이 있으면 뉴런들은 그 자극을 뇌로 전달해서 우리가 느낄 수 있는 것이다. 하지만 뉴런들도 어느정도 강한 자극이 있거나 특정 임계점의 에너지가 작용해야 자극을 전달할 수 있다.
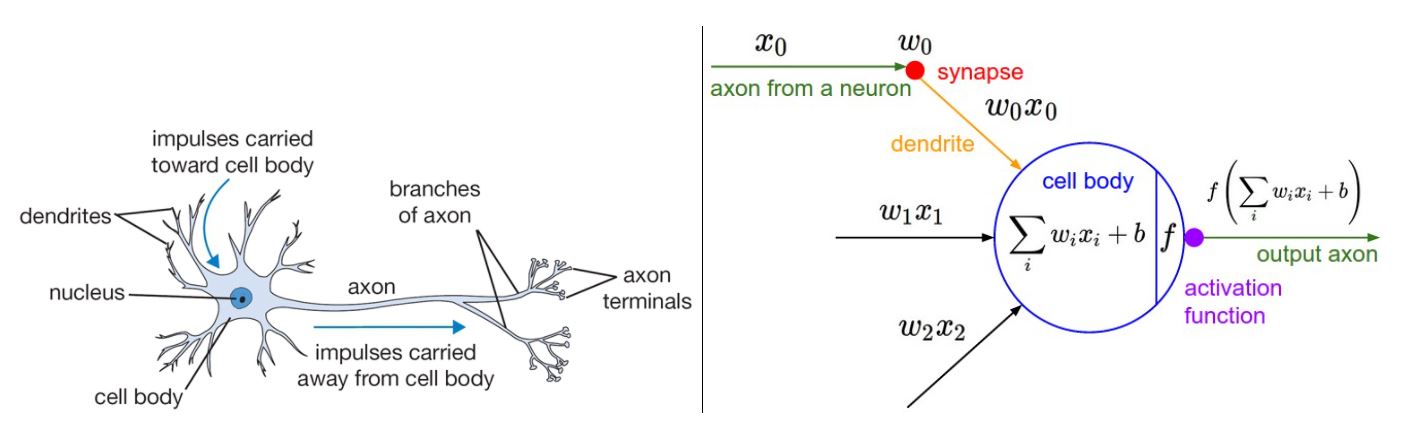
뉴런의 원리가 딥러닝에서도 똑같이 적용이 되는데, 이처럼 특정한 임계값을 넘겨야만 옆으로 자극(연산결과)을 전달하는 것을 활성화 함수(Activation Function) 이라고 한다. 즉, 입력 신호의 총합을 출력 신호로 변환할 때 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다.
수식으로 보면 다음과 같다.
\[\begin{aligned} a &= b + w_1x_1 + w_2x_2\\ y &= h(a)\\ \end{aligned}\]위 식에서 가중치가 달린 입력 신호와 편향의 총합이 $a$이고 활성화 함수가 $h(x)$이다. $h(x)$가 임계값을 경계로 출력값을 바꾸기 때문에 ‘활성화’를 한다고 볼 수 있는 것이다.
활성화 함수의 가장 큰 특징 중 하나는 비선형 함수 를 이용한다는 것이다. 다시 말하면 선형 함수를 사용해서는 안 된다. 그 이유는 신겸앙의 층을 깊게 하는 의미가 없어지기 때문이다. 아래는 선형함수인 $h(x) = cx$를 사용했을 때의 수식이다.
위의 식처럼 은닉층이 없는 네트워크로 표시할 수 있다. 다시 말해 딥러닝 모델을 아무리 깊게 쌓아도 결국 1층 뿐인 것과 같은 효과가 나타나는 것이다. 따라서 모델의 층을 깊게 쌓는 혜택을 얻기 위해서는 활성화 함수를 비선형 함수로 사용해야 한다.
활성화 함수 종류
활성화 함수에 대해 알아보았다. 그렇다면 종류에는 어떤 것들이 있을까?
계단 함수
비선형 활성화 함수 중 가장 간단한 함수이다. 어느 특정 입력값이 넘기 전까지 0 또는 다른 상수로 일정하다가 어느 값 이상이 되면 비연속적으로 증가하는 함수를 말한다.
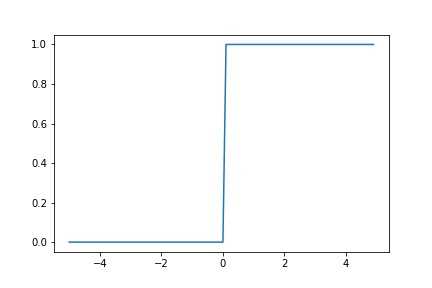
위 그림과 같이 함수 모양이 마치 계단처럼 생겼기 때문에 ‘계단함수’라고 불린다. 하지만 이 함수는 딥러닝의 시초인 ‘퍼셉트론’에서 사용하는 활성화 함수이고, 현재 딥러닝에서는 사용하지 않는다. 출력값이 급격하게 변하면서 많은 데이터의 손실히 발생할 가능성이 있기 때문이다.
시그모이드(Sigmoid) 함수
다음은 계단함수와 다르게 비교적 연속적인 비선형 함수인 시그모이드 함수이다.
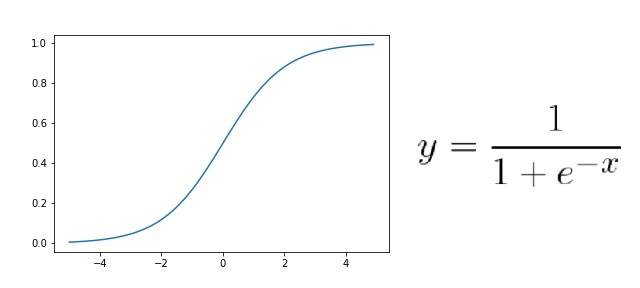
시그모이드 함수의 특징으로는 계단함수보다 더 정교하고 자세한 ‘수치’를 표시할 수 있다는 것이다. 0 또는 1처럼 비연속적이지 않고 0.231처럼 연속된 값으로 표현되기 때문에 데이터에 대한 신뢰도가 더욱 상승한다.
하지만 아쉽게도 시그모이드 함수 또한 문제점을 가지고 있다. 입력값이 0에서 멀어질수록 미분값이 계속 작아져서 가중치 업데이트가 제대로 이루어지지 않는 기울기 손실(Gradient Vanishing) 문제가 발생한다. 경사하강법에서 가중치와 그 가중치의 미분값과 곱하면서 가중치를 갱신하는데, 여기서 0보다 작은 미분값을 계속 곱하다 보면 가중치값이 계속 작아져 제대로 갱신되지 않는 문제가 발생한다.
하이퍼볼릭 탄젠트(Tanh) 함수
시그모이드 함수의 또 다른 단점은 0과 1사이의 값으로 데이터를 한정한다는 데에 있다. 따라서 이 문제를 해결하기 위해 하이퍼볼릭 탄젠트 함수가 제안되었다.
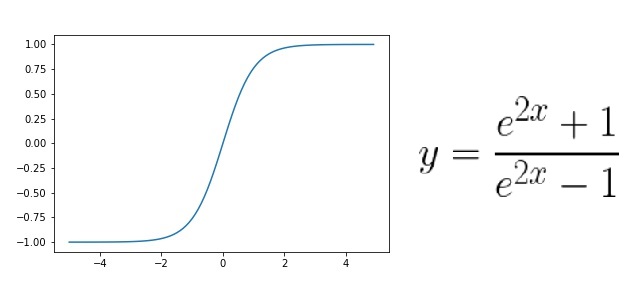
시그모이드 함수에 비해 출력값의 범위도 넓고 기울기의 변화가 더 크기 때문에 학습을 하는데 있어서 손실함수의 최솟값으로 더 빨리 다가갈 가능성이 있다. 하지만 아쉽게도 이 함수 또한 Gradient Vanishing 문제를 해결하지는 못 했다.
ReLU(Rectified Linear Unit)
위에서 언급한 활성화 함수들의 가장 큰 문제점은 Gradient Vanishing 문제를 해결하기 위해 ReLU 함수가 제안되었다.
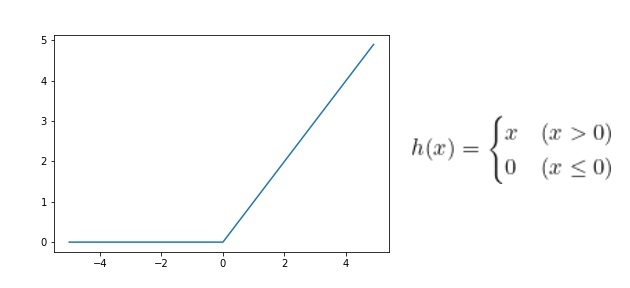
그래프와 수식만 봐도 매우 간단한 함수인 것을 알 수 있다. 입력값이 0보다 크면 입력값 그대로 출력을 하고, 0보다 작으면 모두 0으로 출력한다.
ReLU 함수의 특징은 다음과 같다.
- 본질적으로는 비선형 함수에 속한다.
- ReLU 함수들의 조합 또한 비선형이다.
- 0보다 작은 값들을 0으로 출력하기 때문에 뉴런들을 제거함으로써 계산의 효율을 높인다.
(모델이 가벼워진다.) - 0보다 작은 값들은 0으로 출력하기 때문에 Gradient Vanishing 문제를 해결할 수 있다.
- 기울기값이 1이기 때문에 연산도 매우 간단하다.
ReLU 함수의 단점은 다음과 같다.(“but nothing is flawless”, 완벽한 건 없다.)
- 0보다 작은 값들에 대해서 Gradient Vanishing 문제가 발생하지는 않지만 애초에 오차값이 전달되지 않는 문제가 발생한다.(dying ReLU Problem)
Pytorch 코드 실습
시그모이드(Sigmoid) 함수
import torch
import torch.nn as nn
tensor = torch.randn(2)
sigmoid_func = nn.Sigmoid()
>>> print(tensor)
>>> print(sigmoid_func(tensor))
# tensor([-0.8475, 0.2985])
# tensor([0.2999, 0.5741])
torch.randn(x): $N(0,1)$ 정규화 된 랜덤값을 출력한다.
하이퍼볼릭 탄젠트(Tanh) 함수
tensor = torch.randn(2)
tanh_func = nn.Tanh()
>>> print(tensor)
>>> print(tanh_func(tensor))
# tensor([ 0.2847, -0.8942])
# tensor([ 0.2772, -0.7135])
ReLU 함수
tensor = torch.randn(4)
relu_func = nn.ReLU()
>>> print(tensor)
>>> print(relu_func(tensor))
# tensor([-0.7185, 2.8861, -0.1147, -0.5199])
# tensor([0.0000, 2.8861, 0.0000, 0.0000])
실제로 딥러닝 모델을 정의할 때 활성화 함수는 다음과 같이 사용된다.
(아래 식에 대한 자세한 내용은 여기를 참고하세요.)
# Make Model
import torch.nn as nn
import torch.nn.functional as F
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.conv1 = nn.Conv2d(1, 10, 7, padding = 3)
self.conv2 = nn.Conv2d(10, 50, 7, padding = 3)
self.conv3 = nn.Conv2d(50, 120, 7, padding = 3)
self.conv4 = nn.Conv2d(120, 100, 5)
self.conv5 = nn.Conv2d(100, 20, 5)
self.conv6 = nn.Conv2d(20, 10, 5)
self.conv7 = nn.Conv2d(10, 10, 3)
self.pool = nn.MaxPool2d(2,2)
self.fc1 = nn.Linear(10 * 8 * 8, 120)
self.fc2 = nn.Linear(120, 360)
self.fc3 = nn.Linear(360, 50)
self.fc4 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(self.conv1(x)) # 28 28
x = F.relu(self.conv2(x)) # 28 28
x = F.relu(self.conv3(x)) # 28 28
x = F.relu(self.conv4(x)) # 24 24
x = F.relu(self.conv5(x)) # 20 20
x = self.pool(F.relu(self.conv6(x))) # 8 8
x = x.view(-1, 10 * 8 * 8)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = self.fc4(x)
return x
model = MyModel()
forward() 함수를 정의할 때 각 Convolution Layer와 Linear Layer의 결과가 ReLU 함수의 입력값으로 들어간 후에 출력이 된다. 거의 모든 Layer에 대해 활성화 함수(지금의 경우는 ReLU)를 적용한다. 비선형 함수인 활성화 함수들을 여러개 사용하면서 모델을 복잡하게 만들면 연산량이 많아지는 단점이 있지만 그만큼 복잡한 문제를 해결하는데에 더욱 유리하다.
지금까지 활성화 함수가 무엇이고 어떤 종류가 있는지에 대해 알아보았다. 사실 저 함수들은 꽤 오래 전부터 연구되었고 사용되어진 함수들이다. 지금은 더욱 많은 함수들이 각각의 문제들을 해결하기 위해 제안되고 있다. 이번 포스터에서는 활성화 함수의 ‘시초’라고 할 수 있는 간단한 함수들만 소개를 했다. 다른 포스터에서 좀 더 최신화되고 좋은 활성화 함수를 소개해보도록 하겠다.