이번 포스터에서는 Segmentation모델 중 하나인 U-Net에 대해 알아보자. U-Net은 U-Net: Convolutional Networks for Biomedical Image Segmentation라는 논문을 통해 발표되었다. 특히 biomedical image segmentation에서 좋은 성능을 보인 모델이다. 또한 data augmentation을 이용해 적은 양의 데이터셋으로 좋은 성능을 보인 모델이기도 하다.


U-Net 개요

보통 딥러닝 모델을 다룰때는 많은 양의 데이터셋이 필요하다. 왜냐하면 모델에는 최적화가 필요한 무수히 많은 파라미터들이 존재하기 때문이다. 물론 ImageNet에는 무수히 많은 데이터셋이 있고, 그 밖에도 coco나 pascal 등 다양한 데이터셋이 존재한다. 하지만 U-Net모델을 적용한 분야는 biomedical image이다. 특히 미생물을 다뤘는데, 아쉽게도 이 분야는 데이터셋이 많이 부족했다. 또한 각 세포들을 구별하기 위해서는 classification이 아닌 Segmentation으로 문제를 해결해야하는데, 이것 때문에 더욱 데이터셋 확보가 어려웠다. 그래서 U-Net은 이러한 문제를 해결하기 위해 다양한 테크닉을 선보였다. 테크닉은 다음과 같다.


  • U자 형태의 모델 구조
  • Overlap-tile 전략
  • Elastic Deformation(Agumentation)
  • Weight map


U-Net 구조

U-Net의 구조를 보면 다음과 같다.



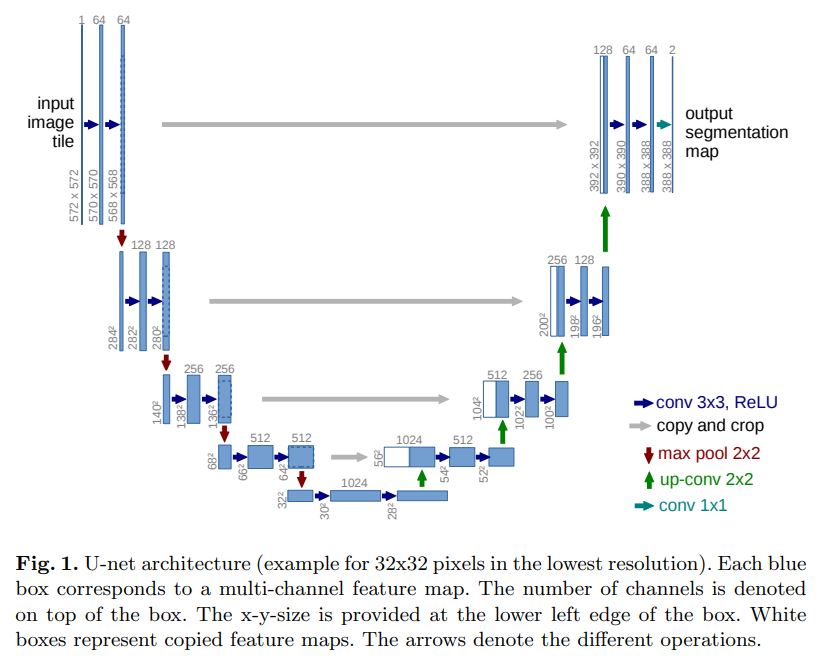
FCN모델을 발전시킨 U-Net의 가장 큰 특징은 U자 형태로 대칭을 이루고 있다는 것이다. 왼쪽은 Downsampling을 통해 feature map을 생성하는 Contracting path이고, 우측은 Downsampling에서 추출한 feature map과 결합하면서 Upsampling을 진행하는 Expansive path이다. 그리고 두 경로가 전환되는 부분이 있다. 각 단계의 구조는 다음과 같다.


  • Contracting path
    • 3x3 Unpadded Convolution 2개, ReLU 2개, 2x2 Maxpooling layer 1개가 결합된 형태 4개
    • Channel이 2배씩 증가
    • Size는 2배씩 감소(Maxpooling 시)
  • Expansive path
    • 3x3 Unpadded Convolution 2개, ReLU 2개, 2x2 Up-Convolution layer 1개가 결합된 형태 4개
    • Channel수는 유지(Up-Convolution layer결과(1/2) + Contracting path feature map)
    • Contracting path에서 추출된 featrue map은 crop을 통해 Expansive path의 feature map과 사이즈를 일치시킴
    • Size는 2배씩 증가(Up-Convolution 시)
  • 전환되는 부분
    • 3x3 Unpadded Convolution 2개, ReLU 2개가 결합된 형태 1개
    • Channel수 2배 증가
    • Size는 감소(Unpadded Convolution)


가장 큰 특징은 Contracting path에서 추출된 feature map이 Expansive path의 feature map과 결합된다는 것이다. U-Net의 구조를 보면 두 path가 대칭구조를 이루고 있는데, 각각 대응되는 feature map이 결합된다. 따라서 Expansive path에서는 Up-Convolution에 의해 channel수가 직전에 비해 2배가 감소하지만, Contracting path의 feature map이 결합되면서 Channel수는 동일하게 유지된다.


Downsampling에서 추출된 feature map을 Upsampling에 결합하기 때문에 더 정확하고 높은 해상도의 Segmentation Map을 예측할 수 있다. 또한 FC Layer를 사용하지 않았기 때문에 Input Image의 전체 Context를 사용할 수 있다.


Output


U-Net은 Segmentation을 수행하는 모델이기 때문에 마지막에 출력되는 Output의 Channel수는 Class의 수가 동일하다. 위 사진에서는 background와 1종류의 세포만 다뤘기 때문에 2개의 Channel이 출력됐다. Class의 수만큼 Channel을 생성하기 위해 1x1 Convolution Layer를 사용한다.


결과적으로 Input Image의 사이즈와 Output의 사이즈가 다른데, 이것은 Padding을 적용하지 않은 Convolution Layer를 사용했기 때문이다.


Overlap-tile

Slide-window 방식과 유사하게 patch 단위로 이미지를 잘라 input data로 사용을 했다. 하지만 Overlap-tile방식은 overlap되는 비율이 Slide-window에 비해 현저히 낮다. 그래서 속도가 월등히 빠른 장점이 있다.


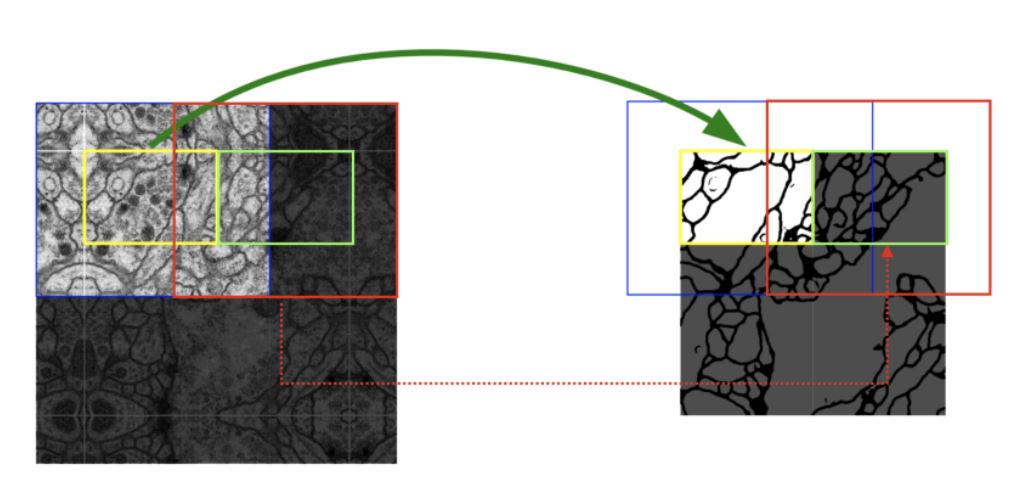
출처 : https://medium.com/@msmapark2/u-net-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0-u-net-convolutional-networks-for-biomedical-image-segmentation-456d6901b28a


위 사진에서 실제 Input data로 사용되는 부분은 파란색과 빨간색 bbox이고, Output은 노란색과 초록색 bbox가 된다. Padding이 없는 Convolution Layer(Valid Convolution)을 사용했기 때문에 Output보다 Input의 사이즈를 크게 설정했다. 두 번째 Tile(빨간색)이 Input image로 사용될 때 첫 번쨰 Tile(파란색)과 겹치는 부분이 있기 때문에 Overlap-Tile이라고 부른다.


Mirror Extrapolate


Input의 사이즈를 키우는 방법에는 여러가지가 있다. 우리가 흔히 알고 있는 Zero-padding의 경우 image 또는 feature map 주위를 0값으로 채워서 Convolution연산이 진행되도 크기가 줄지 않도록 하는 것이다. 하지만 이 논문에서는 Mirror Extraploate라는 방식을 사용했다. Zero-padding과 유사하지만 0값이 아닌 거울처럼 반사되는 방식을 사용한 것이다.



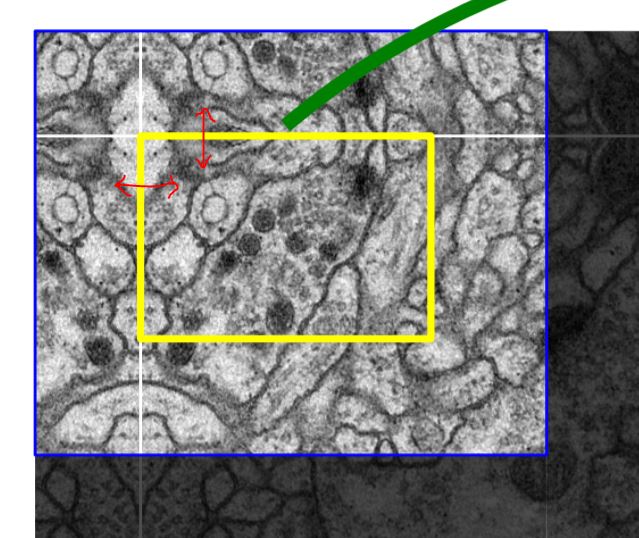
여기서 언급한 Mirror Extraploate는 Convolution Layer에서 말하는 padding과 다른 방식이다. Mirror Extraploate는 단지 Input Image에만 Padding을 적용한 것이고, Convolution에서 padding은 각 Layer가 적용될 떄 Padding을 적용해주는 방식이다. 결론은 U-Net의 경우 Input Image에만 Padding을 적용했고 이후에는 하지 않았다.


Training

학습할 때 특징으로는 다음과 같다.

  • Stochastic Gradient Descent(SGD)
  • Momentum: 0.99
  • Cross Entropy Loss
  • Pixel-wise Softmax
  • Weight Map(Touching Cells)
  • Initialization Weights


Momentum 0.99


Momentum의 경우 매우 큰 값을 사용했는데, 그 이유는 학습이 진행될 때 현재 step이 이전 step의 영향을 많이 받게 하기 위해서이다. 개인적인 생각이지만 Overlap-tile 방식에 의해 1개의 image에서 여러 tile로 쪼개져서 학습이 진행되는데, 이때 현재 tile과 이전 tile이 같은 image내에 있기 때문에 영향을 많이 받게 하기 위해서인 것 같다.


Loss Function


손실함수로는 우리가 흔히 알고 있는 Cross Entropy Loss를 사용했다. 하지만 Segmentation이기 때문에 각 픽셀별로 Backpropagation이 발생한다. 식을 보면 다음과 같다.


\[E=\sum_{\mathbf{x} \in \Omega} w(\mathbf{x}) \log \left(p_{\ell(\mathbf{x})}(\mathbf{x})\right) \\ \quad \\ \begin{aligned} & \mathbf{x}: \text{Pixel} \\ & w: \text{Weight Maps} \\ & p_{\ell}: \text{Pixel-wise softmax에 maximum-function결과} \end{aligned}\]


Segmentation이기 때문에 각 픽셀($\mathbf{x}$)별로 Loss가 산출된다. $w$는 Weight Map으로 세포들의 경계를 더 잘 학습하기 위해 특정 픽셀에 가중치를 더하는 부분이다.


Pixel-wise Softmax


\[p_{k}(\mathbf{x})=\exp \left(a_{k}(\mathbf{x})\right) /\left(\sum_{k^{\prime}=1}^{K} \exp \left(a_{k^{\prime}}(\mathbf{x})\right)\right) \\ \quad \\ \begin{aligned} & \mathbf{x}: \text{Pixel} \\ & a_{k^{\prime}}: \text{픽셀별 output값} \\ & K: \text{class의 개수(= output의 channel 개수)} \\ & p_{\ell}: \text{Pixel-wise softmax에 maximum-function결과} \end{aligned}\]


pixel-wise softmax로 output의 channel이 class의 개수만큼 출력되고, 각 channel이 1개의 class를 나타낸다고 할 때 1개의 픽셀위치에 있는 모든 channel에 대해 softmax를 취하는 방식이다.


Weight Map(Touching cells)


논문에서 Touching Cells이라는 용어를 사용했다. Biomedical Segmentation의 가장 큰 Challenge 중 하나는 각 세포별로 구분히 되어야하는데, 그러기 위해서는 각 세포의 경계가 확실히 나눠져야한다. 따라서 U-Net은 Loss Function에 $w$값을 추가해 원하는 위치의 픽셀값에 더 큰 가중치를 가해 명확히 경계가 구분될 수 있도록 조치했다. Weight Map의 식은 다음과 같다.


\[w(\mathbf{x})=w_{c}(\mathbf{x})+w_{0} \cdot \exp \left(-\frac{\left(d_{1}(\mathbf{x})+d_{2}(\mathbf{x})\right)^{2}}{2 \sigma^{2}}\right) \quad \\ \begin{aligned} & \mathbf{x}: \text{Pixel} \\ & w_c: \text{class frequency의 균형을 맞추기 위한 weight map} \\ & w_0: \text{Weight Map 상수} \\ & d_1: \text{현재 픽셀에서 첫 번째로 가까운 세포의 경계까지의 거리} \\ & d_2: \text{현재 픽셀에서 두 번째로 가까운 세포의 경계까지의 거리} \end{aligned}\]


위 식에 의해 세포의 경계와 가까이 있는 픽셀은 큰 가중치값을 가지고, 멀리 있는 픽셀은 낮은 가중치값을 가진다. 이러한 특징 때문에 각 세포들의 경계에 존재하는 픽셀들은 주로 높은 가중치값을 가지게 된다. 따라서 세포들간의 경계를 비교적 명확하게 학습할 수 있다는 장점이 있다.



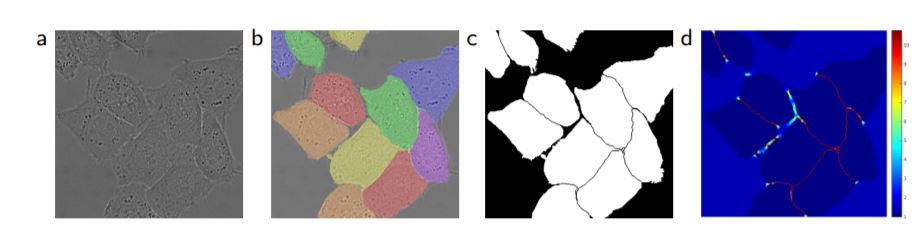
위 사진은 세포가 포함되어 있는 image(a)에 각 instance별로 색깔을 입힌 image(b)과 세포와 배경의 색깔을 흑,백으로 표현한 image(c), 그리고 Weight Map을 시각화한 image(d)이다. 이처럼 Weight Map에 의해 경계부분의 가중치가 더 큰 것을 알 수 있다.


Weights Initalization


U-Net뿐만 아니라 다른 모델들도 가중치의 초기화는 매우 중요한 요소이다. 만약 가중치의 초기화가 제대로 이루어지지 않으면 모델의 특정 부분은 큰 activation값을 가지고, 다른 부분은 매우 작은 activation값을 가지게 되어 쓸모가 없는 Layer가 생겨난다. U-Net은 이러한 문제점을 해결하기 위해 가우시안 분포(Gaussian Distribution)을 이용했는데, 표준편차는 $\sqrt{2/N}$을 적용했다. $N$은 한 Layer의 노드의 개수를 말하는데, 3x3 Filter를 이용한다고 하면 64개의 feature map과 3x3 Filter를 곱해 $64 \cdot 9 = 576$가 된다.


Elastic Deformation

U-Net의 가장 큰 특징 중 하나는 적은 데이터셋으로 좋은 성능을 보인 것이다. Biomedical의 특성 상 학습에 사용할 데이터가 매우 적은데, 이 문제를 해결하기 위해 Augmentation의 기법 중 하나인 Elastic Deformation을 이용했다.



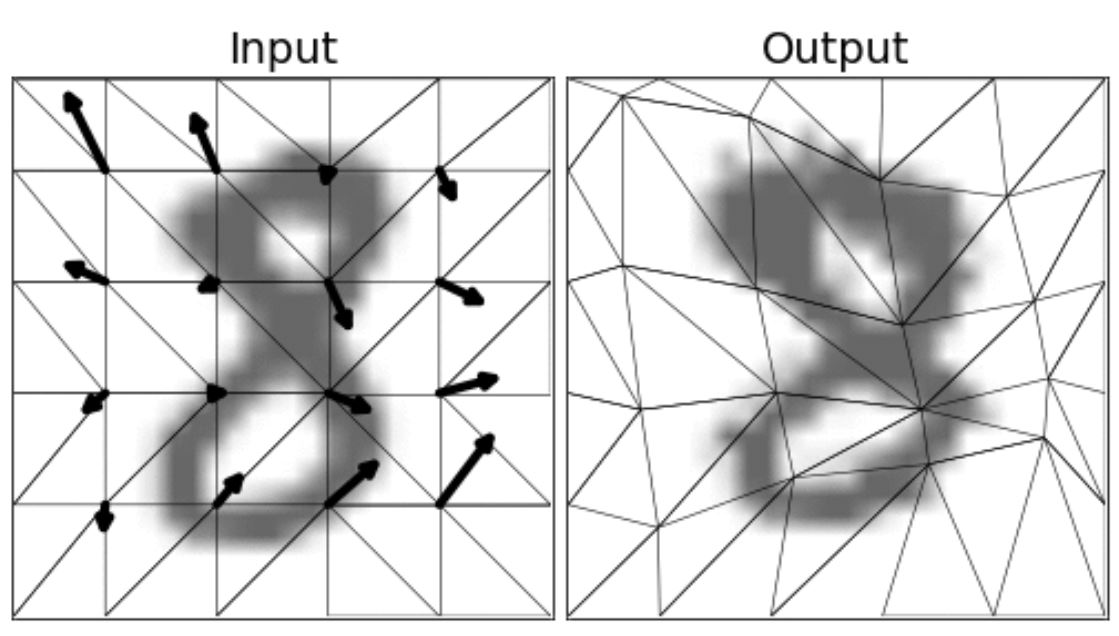
Affine Transform에 Probalilistic spin을 적용한 방식인 Elastic Deformation은 각 픽셀별로 뒤틀리는 특징이 있다. Biomedical Image의 경우 세포들의 움직임과 변형이 Elastic Deformation과 비슷한 양상을 보이기 때문에 매우 좋은 Augmentation기법이다.


Experiments

이전의 연구들과의 차이를 보면 U-Net이 월등히 좋은 성능을 보인다. 아래는 PhC-U373과 DIC-HeLa데이터셋에 대한 모델들의 성능비교이다.



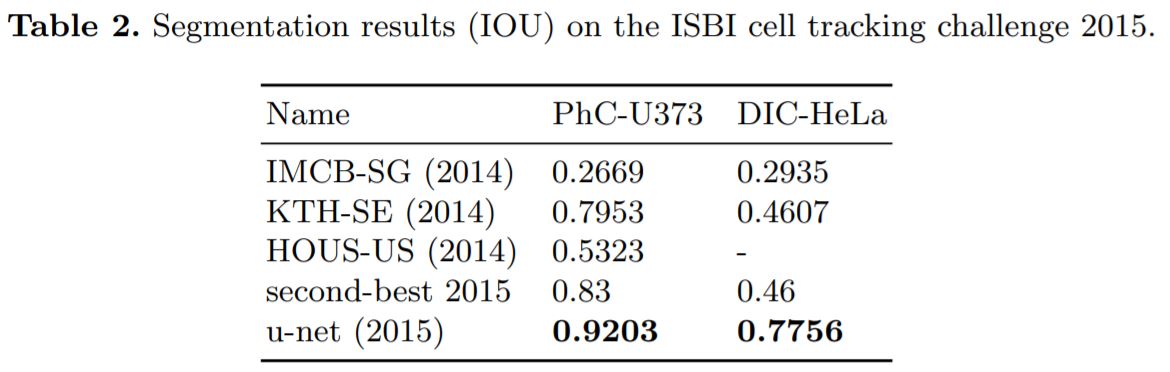
지금까지 U-Net에 대해 알아보았다. U-Net은 Biomedical image에 특화된 모델을 만들기 위해 노력한 것처럼 보인다. 하지만 Biomedical뿐만 아니라 Segmentation분야에 전반적으로 좋은 인사이트를 주었다.


읽어주셔서 감사합니다.(댓글과 수정사항은 언제나 환영입니다!)