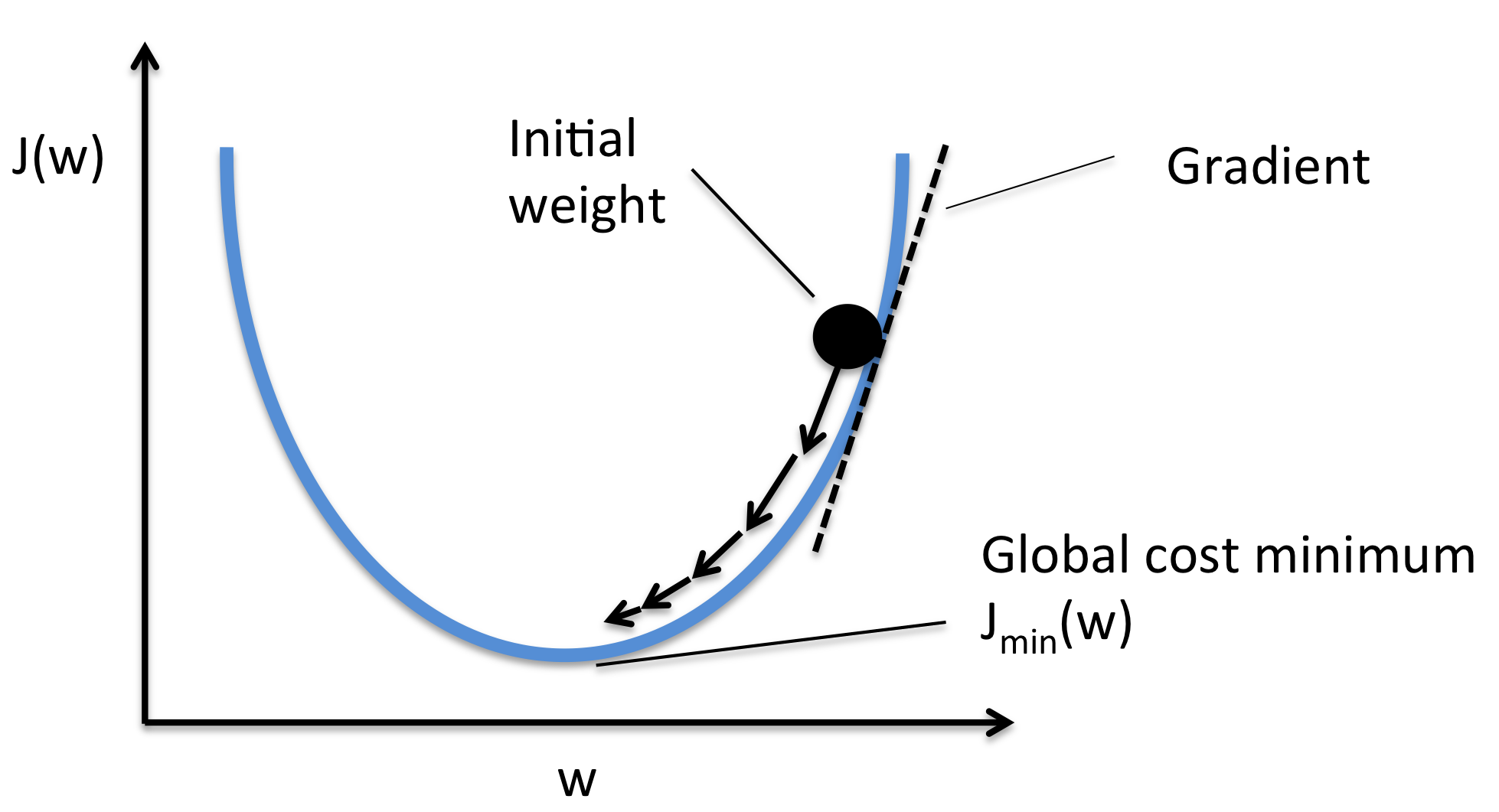
신경망이 학습을 하는 원리는 기본적으로 ‘모델 f(x)가 입력 x에 대해 적절한 예측값인 y을 출력하게 하는 모델 f(x)의 구성품인 매개변수(가중치)을 정하는 작업’이다. 데이터를 입력하고 나온 결과인 예측값과 정답값을 비교하여 그 차이인 Loss값을 구하고 그 값을 최소화하는 방향으로 학습을 하게 된다. 즉, Loss값을 최소화하기 위해 loss값의 함수인 ‘손실함수’를 사용한다. 신경망 학습에서는 최적의 매개변수(가중치)를 탐색할 때 손실 함수의 값을 가능한 한 작게 하는 매개변수(가중치)를 찾는다. 즉, Loss에 대한 각각의 매개변수의 미분을 계산하고, 그 미분 값을 서서히 갱신하여 최적의 매개변수를 찾는 과정으로 학습을 한다.

그렇다면 왜 ‘정확도’라는 지표를 두고 ‘손실 함수’라는 우회적인 방법을 택하는 것일까요?

만약 ‘정확도’를 지표로 사용을 한다면 위에서 언급한 ‘미분’값이 대부분의 장소에서 0값이 되기 때문이다. 예를 들어 100장의 사진을 예측했는데 32장만 올바르게 예측했다면 이 모델은 32%의 정확도를 띈다. 하지만 정확도를 향상시키기 위해 가중치 매개변수의 값을 조금 바꾼다고 해도 일정하게 유지하는 경향이 있고, 값이 바뀐다고 하더라도 35.12355…% 와 같은 연속적인 숫자보다도 37%, 38% 등의 불연속적인 값으로 바뀐다. 따라서 효율적인 학습을 위해 Loss값을 이용한 ‘손실 함수’를 지표로 이용하게 된다.

미분

미분의 기본 개념은 ‘함수 $f(x)$에 대해 $x$가 변할 때 $f(x)$가 변하는 정도’이다. $x$ 지점에서 $f(x)$의 변화율을 뜻한다. $f(x)$의 미분은 $\frac{\partial y}{\partial x}$로 나타낼 수 있고 이것이 $x$지점에서 $f(x)$의 접선의 기울기이다.
미분값은 다음과 같이 계산한다.

\[\frac{\partial y}{\partial x} = \lim_{h \rightarrow 0}\frac{f(x+h) - f(x)}{h}\]

Python으로 위 식을 계산하면 아래와 같다.

\[\left\{ \begin{array}{ll} x = 1 \\ y = 3(x+1)^2\\ \end{array} \right.\]

def f(x):
    y = 3*(x+1)**2
    return y

def diff(F, X):
    h = 0.001 # 매우 작은 수
    return (f(x+h) - f(x)) / h

x = torch.ones(1)
d = diff(f, x)
>>> print(d)
# tensor(12.0020) # 12에 근사한 값

따라서 우리는 위의 식을 이용해 기울기를 구하고, 매개변수들을 조금씩 변화시키면서 손실함수의 값이 최소가 되는 지점을 찾아야 한다. 여러가지 방법이 있지만 그 방법에 대해서는 나중에 다룰 예정이고, 이번 포스트에서는 미분값을 쉽게 구하는 방법에 대해 얘기할 것이다.

AutoGrad

Pytorch에서는 이러한 ‘미분’값을 쉽고 빠르게 구할 수 있도록 하는 자동미분 기능을 제공한다.

앞에서 배웠던 torch.Tensor() 클래스로 Tensor을 생성
클래스 안에 .requires_grad 속성을 True로 설정하면 자동미분 기능을 켤 수 있다.
자동미분이 적용되는 Tensor의 모든 연산을 추적한다.
계산이 완료되면 .backward()를 호출하여 변화도(미분)를 자동으로 계산할 수 있다.
loss값에 대한 미분이기 때문에 자동미분을 계산하기 전에는 1개의 값으로 나와야한다.(Scalar)

\[\left\{ \begin{array}{ll} x = 1 \\ y = 3(x+1)^2\\ \end{array} \right.\]

위의 식을 예로 코드를 작성해보자.

import torch
x = torch.ones(1, requires_grad=True) # 2x2 행렬(값이 모두 1)
>>> print(x)                            # requires_grad=True로 자동미분 실행
# tensor([1.], requires_grad=True)

y = 3 * x**2
y.backward() # y에 대한 x의 기울기 계산

>>> print(x.gard) # y에 대한 x의 기울기 출력
# tensor([12.])

위 코드에서 볼 수 있듯이 .backward()을 호출하여 기울기를 쉽게 계산하고 $x$.grad()을 통해 $f(x)$에 대한 $x$의 기울기가 12임을 출력한다. 위 예시는 너무 간단했기 떄문에 좀 더 복잡한 식에 대한 기울기를 구해보았다.

\[x= \begin{Bmatrix} 1 &1 &1 &1 \\ 1 &1 &1 &1 \\ 1 &1 &1 &1 \\ 1 &1 &1 &1 \end{Bmatrix}, \quad y = x^4 + 3x^3 + 8x^2 + 3\]

자동미분을 이용하지 않고 수치미분으로 계산하는 코드는 아래와 같다.

def f(x):
    y = x**4 + 3*x**3 + 8*x**2 + 3
    return y

def diff(F, X):
    h = 0.00001 # 매우 작은 수
    return (f(x+h) - f(x)) / h

x = torch.ones(4,4)
d = diff(f, x)

>>> print(d/16) # x의 요소의 개수 = 16개
# tensor([[1.8120, 1.8120, 1.8120, 1.8120],
#         [1.8120, 1.8120, 1.8120, 1.8120],
#         [1.8120, 1.8120, 1.8120, 1.8120],
#         [1.8120, 1.8120, 1.8120, 1.8120]])

아래의 코드는 자동미분을 이용하여 계산하는 코드이다.

x = torch.ones(4,4, requires_grad=True)
y = (x**4 + 3*x**3 + 8*x**2 + 3).mean() # 자동미분은 scalar값에 대해서만 계산이 가능하다.
y.backward()

>>> print(x.grad)
# tensor([[1.8120, 1.8120, 1.8120, 1.8120],
#         [1.8120, 1.8120, 1.8120, 1.8120],
#         [1.8120, 1.8120, 1.8120, 1.8120],
#         [1.8120, 1.8120, 1.8120, 1.8120]])

이번 포스터를 통해 미분에 대해 간단히 알아보았고 Pytorch을 이용해 미분값을 빠르게 찾을 수 있는 Autograd 기능을 알아보았다. 나중에 인공신경망을 통해 학습을 하고 예측을 할 때 매우 유용하게 쓰일 것으로 예상이 된다. 사실 이번 포스터를 통해 Autograd을 활용하는 방법에 대해 정확하게 알았고 여러 포스터들을 참고하다보니 새로운 사실들도 많이 알게 되었다. 딥러닝 모델을 이용하여 진행한 프로젝트도 업로드할 예정인데, 프로젝트를 할 때 이러한 개념들이 많이 사용될 것으로 생각이 된다.
다음 포스터에서는 Pytorch을 이용하여 실제로 간단한 모델을 만들어보고 forward() 계산이 되는 방식에 대해 알아보도록 하자.

미분

AutoGrad

읽어주셔서 감사합니다.(댓글과 수정사항은 언제나 환영입니다!)