이번 포스트에서는 Object Tracking모델에서 자주 사용되는 Kalman Filter(칼만 필터)에 대해 알아보자. 칼만 필터를 깊히 이해하기 위해서는 수많은 수식과 배경지식이 필요하지만, 여기서는 사용할 수 있는 정도로만 이해를 하고자 한다. 칼만필터에 사용되는 많은 식들이 어떻게 유도되었는지는 자세히 다루지 않고, 프로세스가 작동하는 원리를 이해하는데 초점을 맞췄다.

Kalman Filter(칼만 필터)

칼만 필터란 ‘잡음이 포함되어 있는 측정치를 바탕으로 선형 역학계의 상태를 추정하는 재귀 필터’이다. 루돌프 칼만이 개발한 필터로 과거에 수행한 측정값을 바탕으로 현재의 상태 변수의 결합분포를 추정한다. 여기서 ‘측정치’는 어떠한 현상을 관찰하고 얻은 데이터이고, ‘잡음’은 데이터를 수집할 때 발생하는 여러 오차(관측 오차, 기계 오차 등)를 뜻한다.

이름에 필터라는 단어가 들어가는데, 과거의 데이터로부터 현재를 추정할 때 포함되어 있는 노이즈를 정제하는 역할을 수행하기 때문이다. 모든 측정치는 ‘잡음’이 반드시 포함되기 마련인데, 이러한 ‘잡음’을 정제하여 예측의 정확도를 높이는 기법이다.

예를 들어 Object Tracking 모델에서 이전 frame에서 탐지된 object가 현재 frame에서 어느 위치에 존재할지 예측하는 경우 칼만 필터가 사용된다. 사람을 탐지한다고 했을 때 사람이 일정한 속도로 이동한다는 시스템 모델을 이용해 현재 frame에서 동일한 사람의 위치를 예측하는 것이다.

칼만 필터는 다양한 분야에 사용되지만, 이 포스터에서는 Object(People) Tracking에서 사용한다고 가정한 상태에서 설명을 진행할 예정이다.

Kalman Filter 구성요소

칼만 필터는 크게 2가지 단계로 이루어져있다. 이전 Frame에서 특정 위치에 존재하던 사람이 현재 Frame에서 어디에 위치하게 되는지 예측하는 상태 예측(predict)과 현재 Frame에서 예측한 사람의 위치와 실제 측정값(Detection 결과)을 비교하여 보정하고 ‘잡음’을 계산하는 측정 업데이트(update)단계가 있다.

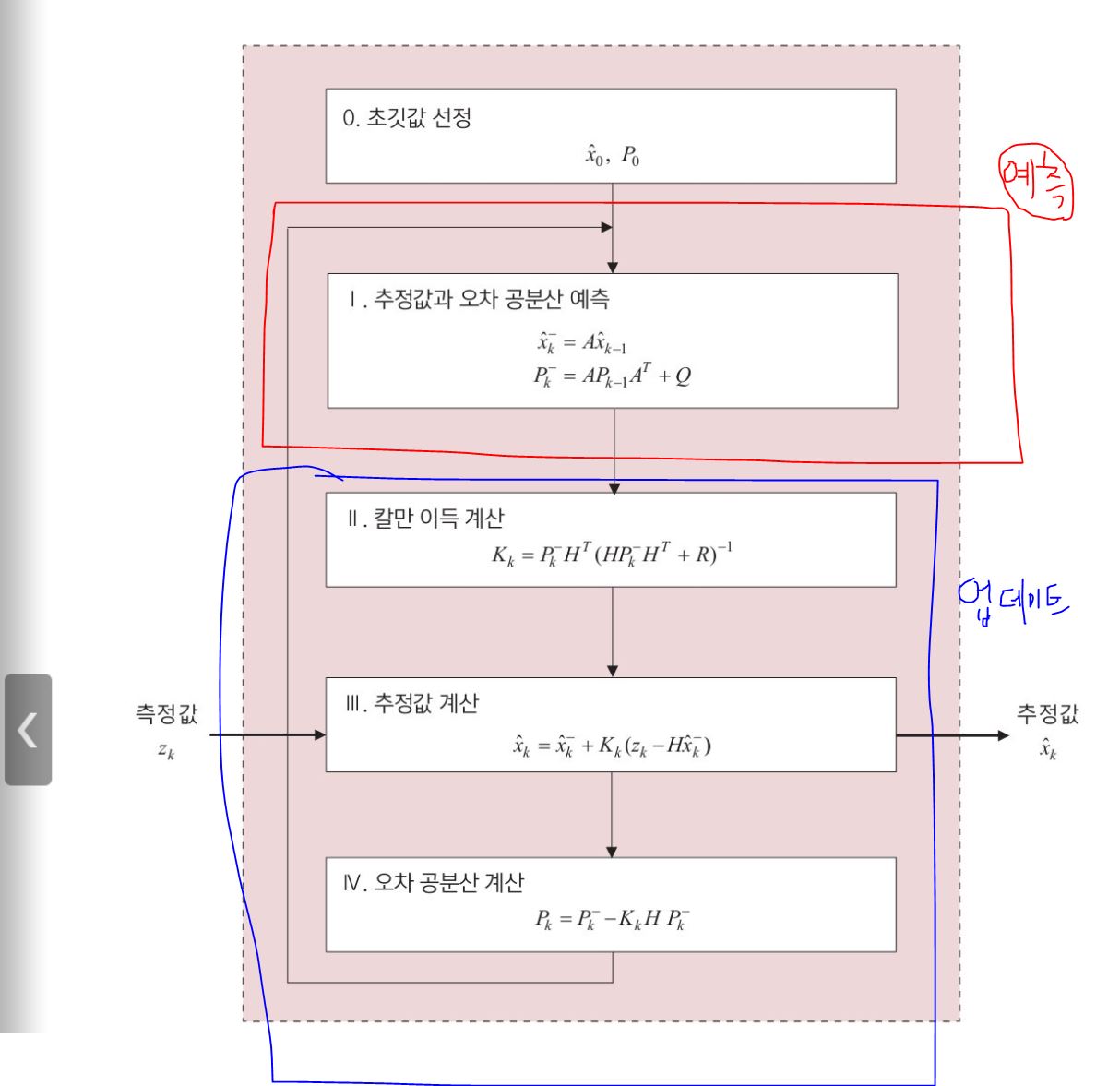
출처 : https://fliphtml5.com/hkuy/zyfj/basic

칼만 필터를 검색하면 차근차근 설명된 자료가 없고 위와 같이 수식만 나열해놓은 모습을 볼 수 있는데, 칼만 필터의 컨셉만 이해해도 충분히 사용할 수 있었다.

이해를 돕기 위해 사진에서 사용된 문자들을 정의하면 다음과 같다.(People Tracking을 가정)

$\hat{x}_k^-$ : 과거 frame으로부터 예측한 위치정보
$\hat{x}_k$ : 현재 Frame의 위치정보를 보정한 값
$P_k^-$ : 과거 frame으로부터 예측한 위치정보에 대한 오차값(공분산 오차)
$K_k$ : 측정 오차(Kalman Filter)와 관측 오차(Detection)의 비율(칼만 이득)
$H$ : 행렬에서 관측값과 예측값을 이어주는 보조행렬(measurement function)

상태 예측(Predict)

과거 Frame에 있던 사람의 위치정보($\hat{x}{k-1}$)를 이용해 현재 frame에서의 위치($\hat{x}{k}$)를 예측하는 단계이다.

\[\begin{aligned} &\hat{x}_{k}^{-}=A \hat{x}_{k-1} \\ &P_{k}^{-}=A P_{k-1} A^{T}+Q \end{aligned}\]

위 식에서 $A$는 시스템 모델 중 하나로 사람의 움직임을 모델로 표현한 식이다. 즉, 특정 물체의 역학을 이론상으로 표현한 모델이다. 예를 들어 사람이 한 방향으로 등속운동을 한다고 가정하면, $A$는 위치/속도/시간 관계를 나타내는 모델이 될 것이다. 따라서 과거 Frame에서 사람의 위치$\hat{x}_{k-1}$에 시스템 모델$A$를 곱해 현재 Frame에서 사람의 위치를 예측한다.

$P_k^-$는 현재 Frame에서 칼만 필터의 예측 오류값(Estimate Uncertainty)이다. 즉, 각 기계마다 오차가 있듯이 칼만 필터의 오차를 나타낸다. 칼만 필터의 목표 중 하나는 $P$을 낮춰서 필터의 예측능력을 높이는 것이다. 즉, 관측값에 의존하지 않고 오로지 예측값에만 의존할 수 있도록 $P$를 낮추는 것이 목표이다. $Q$의 경우 시스템 노이즈 오차(Process Noise Uncertainty)로 모델을 설계할 때 발생할 수 있는 오차를 말한다. 예측된 $P$는 이후에 칼만 이득(K)를 구하거나 다음 Frame에서의 $P$를 구할 때 사용된다.

측정 업데이트(Update)

이 단계의 목표는 칼만 이득($K$)과 관측값($z_k$)을 이용해 예측값($\hat{x}_k^-$)을 보정($\hat{x}_k$)하고 칼만 필터의 오차($P_k$)를 계산하는 것이다.

\[\begin{aligned} &K_{k}=P_{k}^{-} H^{T}\left(H P_{k}^{-} H^{T}+R\right)^{-1} \\ &\hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right) \\ &P_{k}=P_{k}^{-}-K_{k} H P_{k}^{-} \end{aligned}\]

$K$은 칼만 이득으로,예측 오차(Estimate Uncertainty)와 관측 오차(Measurement Uncertainty)의 관계를 계산한다. 행렬로 표시했기 때문에 매우 복잡해보이지만, 단순하게 다음과 같이 표현될 수 있다.

\[K = \frac{예측 오차}{예측 오차 + 관측 오차}\]

만약 예측 오차가 작고 관측 오차가 크면 K값은 전체적으로 작아지는데, 이는 곳 칼만 필터의 능력이 향상되어 관측치를 보지 않고도 충분히 예측을 할 수 있다는 것을 의미한다. 반대로 예측 오차가 크고 관측 오차가 작으면 K값은 전체적으로 커지는데, 칼만 필터의 능력이 아직 부족해서 보정 시 관측값에 의존을 많이 하게 된다는 뜻이다.

$\hat{x}_k$는 상태 예측단계에서 예측한 $\hat{x}_k^-$값을 관측값($z_k$)과 칼만 이득($K_k$)를 이용해 보정한 값이다. 이 과정에서 현재 Frame의 예측값이 보정되어 다음 frame의 예측값을 계산할 때 적용된다. 예측값과 관측값의 의존성은 칼만 이득($K$)에 의해 영향을 받는다.

$P_k$의 경우 상태 예측단계에서 예측한 오차 공분산인 $P^-_k$을 보정한 값이다. 이 수치는 이후에 칼만 이득($K$)에 영향을 받고, 이후에 칼만 이득(K)을 계산하는데 사용된다.

People Tracking에서의 칼만 필터

최종적으로 칼만 필터가 목표로 하는 것은 관측치를 보지 않고 과거 데이터를 통해 현재 데이터를 추정하는 것이다. 예측과 업데이트를 재귀적으로 반복하면서 관측치의 의존성을 낮추고 오로지 예측만으로 본 적 없는 데이터를 추정하는 것이다. 이러한 기능은 People Tracking을 하는데 매우 유용하다.

Tracking 모델은 여러가지 방식이 있지만, 대표적으로 tracking-by-detection 방식이 있다. 이 모델의 경우 매Frame마다 Detector가 이미지 내에 있는 사람을 탐지하고, 기존에 존재하던 사람과 비교하고 매칭하여 tracking을 실시한다. 이 과정에서 과거 frame과 현재 frame에 있는 사람의 유사도를 측정하는데 있어서 칼만 필터의 결과는 비교의 밑거름으로 사용되고, 만약 Occlusion이 발생하여 일시적으로 존재하던 사람이 보이지 않으면 예측을 통해 자연스럽게 tracking이 될 수 있도록 도와준다. 따라서 칼만 필터는 Tracking 모델을 설계하는데 필수적인 요소 중 하나라고 할 수 있다.

코드로 보는 칼만 필터

Filterpy 라이브러리에서 칼만 필터를 사용할 수 있도록 클래스를 제공해준다. 위에서 언급한 시스템 모델과 각 변수들을 할당할 수 있고, predict()과 update()메소드를 이용해 예측 및 업데이트를 진행할 수 있다.

예시 코드는 다음과 같다.

kf = KalmanFilter(dim_x=6, dim_z=2)

# Variables
kf.F = np.array([[1,1,0.5,0,0,0],[0,1,1,0,0,0],[0,0,1,0,0,0],[0,0,0,1,1,0.5],[0,0,0,0,1,1],[0,0,0,0,0,1]])
kf.Q = np.array([[0.25,0.5,0.5,0,0,0],[0.5,1,1,0,0,0],[0.5,1,1,0,0,0],[0,0,0,0.25,0.5,0.5],[0,0,0,0.5,1,1],[0,0,0,0.5,1,1]])
kf.Q *= 0.5**2
kf.R = np.array([[9, 0], [0, 9]])
kf.H = np.array([[1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]])

# Initalizaiton
kf.x = np.array([0, 0, 0, 0, 0, 0])
kf.P *= 500

# noisy measurements
measurements = load_data()

kf.predict() # x1, p1
estimates = np.zeros_like(measurements)
for idx in range(0, len(measurements)):
    m = measurements[idx]    
    kf.update(m)
    estimates[idx,0] = kf.x[0]
    estimates[idx,1] = kf.x[3]
    
    kf.predict()

임의의 관측값(measurements)에 대해 칼만 필터를 적용한 결과는 다음과 같다.

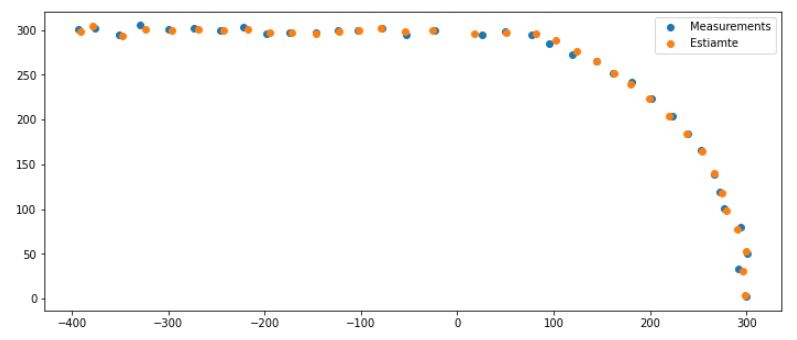
자세한 코드는 여기에서 확인할 수 있다.

지금까지 칼만 필터에 대해 알아보았다. 칼만 알고리즘의 과정이 표시되어 있는 사진을 보면, 매우 복잡하고 이해하기가 어렵다. one-dimensional 문제로 낮춰서 차근차근 해결하면 매우 간단하지만, Multi-dimensional 문제로 일반화를 해서 보기 때문에 매우 어렵게 느껴진다. 특히 다차원을 표현하기 위해 행렬을 이용하다 보니 더욱 어려워보이는 것 같다. 만약 각 식들의 유도과정을 정확하게 알고싶거나 칼만 필터와 관련된 다양한 예시문제를 풀어보고 싶다면 https://www.kalmanfilter.net/ 이곳을 참고하면 좋을 것 같다.