RCNN은 2014년 Rich feature hierarchies for accurate object detection and semantic segmentation라는 논문을 통해 발표되었다. 논문에 대한 리뷰는 여기에서 확인할 수 있다. 이번 포스터에서는 RCNN의 구조에 대해 구체적으로 다뤄볼 예정이다. 논문에서 전반적인 내용을 언급했지만, 하나하나 자세히 다루지 않아 구조를 이해하기 어렵기 때문이다.

RCNN 개요

---

ImageNet Challenge에서 첫 딥러닝 모델인 AlexNet이 좋은 성능을 보이면서 CNN 구조에 대한 연구가 활발히 일어나기 시작했다. AlexNet의 경우 Classification에 적용한 모델이지만, Object Detection분야에서도 CNN구조를 사용하기 위해 많은 노력을 했다. 그 결과 RCNN 이전 CNN과 Sliding Window기법을 이용한 Overfeat Model이 등장하였다. 하지만 Overfeat model은 연산량이 많고 bounding box또한 정확하지 않아 성능이 떨어진다는 평을 받았다.

RCNN은 Overfeat model이 가지고 있는 문제점을 해결한다. 연산량을 줄였고 성능 또한 VOC 2012데이터를 기준으로 30% 이상 향상되었다.

RCNN은 Object Detection 분야의 모델 중 하나로 Region proposal과 CNN feature의 개념을 합친 모델이다. Region Proposal을 한글로 번역하기는 쉽지 않지만, 굳이 표현하자면 ‘이미지 내에 특정 구역을 추출한다’고 할 수 있겠다. 그리고 CNN Layer를 통해 각 region proposal의 feature를 추출하고, Linear SVM과 Bouning box regression을 통해 클래스를 분류하고 네모 상자의 위치를 찾아낸다.

RCNN의 구조

---

RCNN의 구조를 보면 다음과 같다.

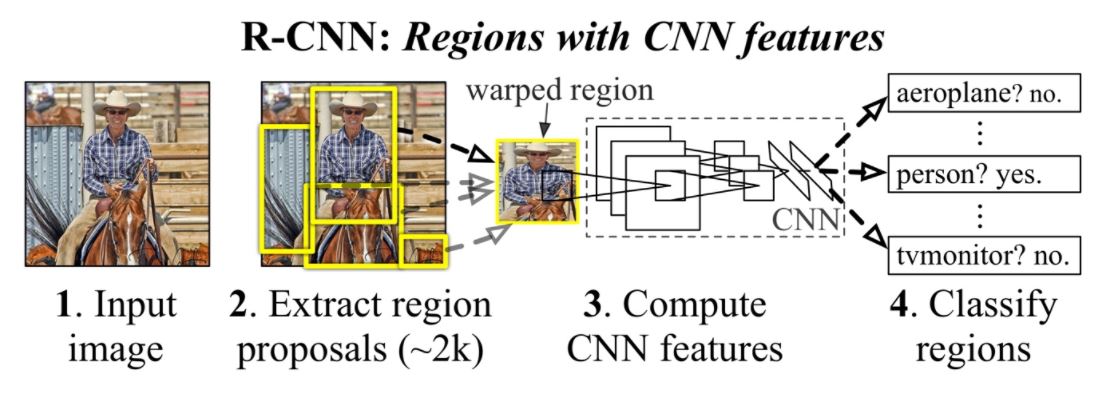
R-CNN의 forward 방식은 다음과 같다.

1. Input 이미지를 입력한다.
2. 이미지 내에서 약 2000개의 Region Proposals를 추출한다.
3. 각 Region Proposal의 feature를 추출한다.
4. Linear SVMs를 이용해 각 Region Proposal를 분류한다.

위 사진은 논문에 기재되어 있는 것이고, 아래 사진은 RCNN모델을 더 구체적으로 표현했다. 여러 과정 중에 대표적으로 3가지만 깊게 알아볼 예정이다.

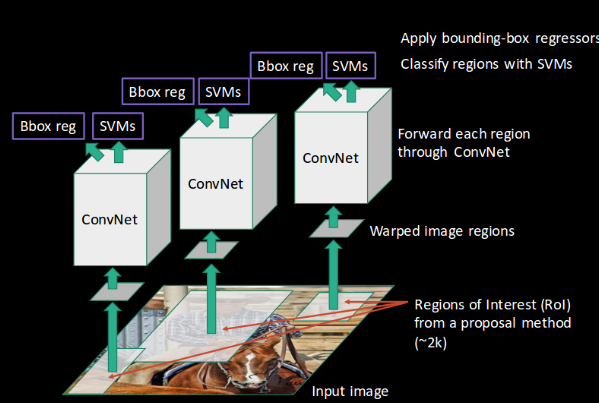
Region Proposal

---

번역해보면 ‘이미지 내에 특정 구역을 추출’하는 부분이다. R-CNN 모델에서는 이미지 내에서 Object의 후보가 될 수 있는 부분을 Selective Search Algorithm을 이용해 추출했다. selective search는 2013년 ILSVRC의 detection 분야에 참가해 Overfeat방식을 누르고 1위를 차지했다. 따라서 이후에 나오는 여러 CNN 모델(R-CNN, SPPNet, Faster R-CNN 등)에 후보 영역을 추출하는데 사용되었다.

Selective Search Algorithm

이미지가 계층적 구조를 가진다는 것을 가정한 상태에서 알고리즘이 적용된다. 이미지에 대해 비슷한 영역끼리 묶어서 segmentation을 실시하고, 영역들을 적절한 기법을 통해 원하는 개수가 나올떄까지 통합해나간다. 그림으로 보면 다음과 같다.

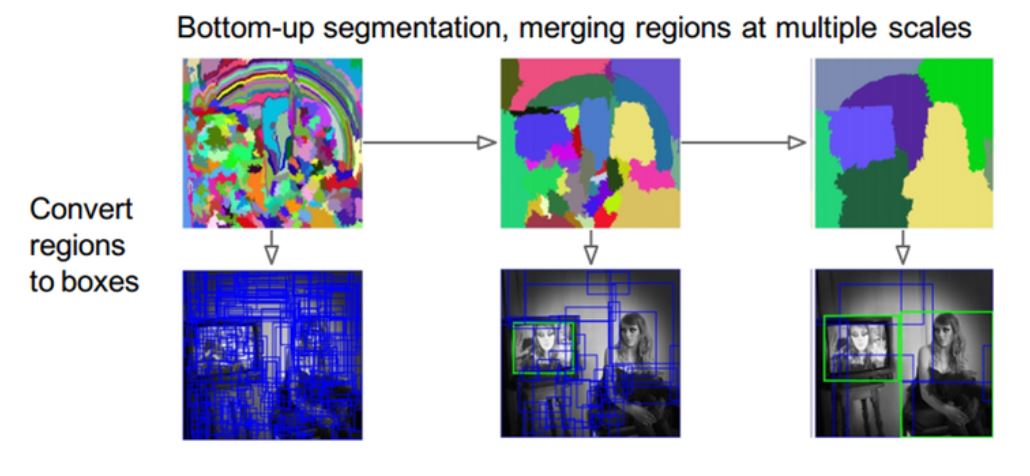
1. 색상, 질감, 영역 크기 등을 이용해 non-objective segmentation을 수행한다.
2. Bottom-up 방식으로 segmentation 조각들을 통합한다.
3. (2) 작업을 반복하여 최종적으로 2000개의 region proposal를 추출한다.

추출된 Region Proposal들은 CNN Layer를 통과하기 전에 모두 동일한 사이즈(227x227)로 Resize해준다. 위 사진에서 ‘Warped image regions’에 해당한다.

CNN Feature

---

CNN의 경우 5개의 CNN Layer와 2개의 Fully-connected Layer를 사용했다. 구조는 AlexNet와 동일하고 Domain-specific fine-tuning방식을 사용했다. 방대한 dataset인 ImageNet을 이용해 CNN구조를 학습하고, 비교적 작은 dataset인 VOC PASCAL를 이용해 fine-tuning을 진행했다. 이후에 2000개의 region proposal(227x227)을 입력받아 4096-dimension의 feature vector를 추출한다.

또 다른 특징으로는 실제 학습을 할 때 IoU(Intersection of Union)을 이용해 Positive와 negative sample를 선정한다.

• Positive sample : region proposals와 ground-thruh box의 Iou값이 0.5보다 큰 sample
• Negative sample : region proposals와 ground-thruh box의 Iou값이 0.5보다 작은 sample
• ground-truth값만 사용하는 것이 아닌 positive를 사용함으로서 데이터를 증가시켜 overfit 방지
• 하나의 미치배치 당 positive 32개, negative 96개로 총 128개를 사용한다.

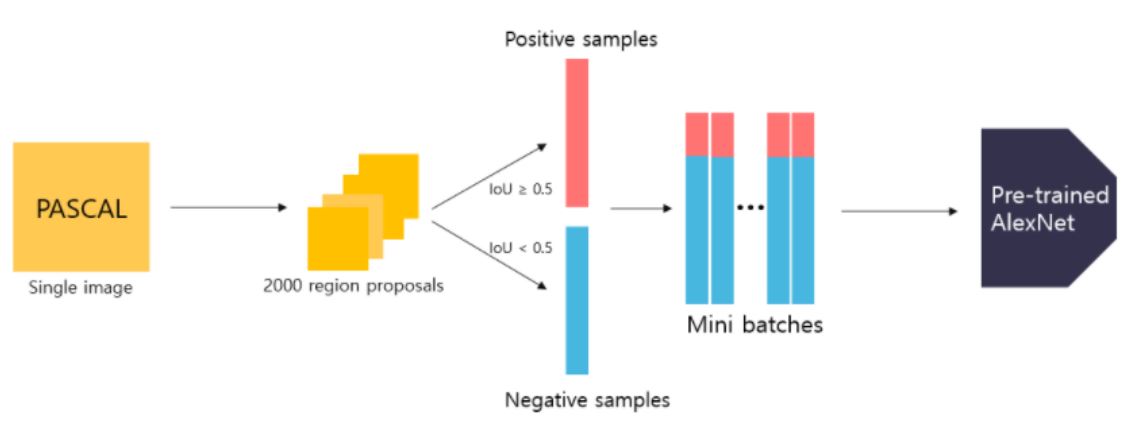
위와 같은 방식을 이용해 domain-specific fine-tuning을 진행할 때 AlexNet의 마지막 layer인 softmax layer를 N(class의 개수) + 1(배경)으로 수정한 후 classification을 수행한다. 하지만 실제로 R-CNN을 사용할 때는 softmax layer는 제거하고 SVM를 사용하기 위해 4096-dimension을 추출한다.

Linear SVMs

---

위에서 진행한 fine-tuning과 다르게 SVMs를 학습시킬 때는 ground-truth만 positive sample로 사용하고, IoU가 0.3보다 작은 경우에만 Negative sample로 사용한다. 똑같이 32개 + 96개 = 128개가 한 개의 배치를 구성하고 있고, CNN 모델에 입력하여 4096-dimension의 feature vector를 추출한다. 그리고 vector를 이용해 Linear SVMs를 학습한다. SVMs의 경우 2진분류를 실시하기 때문에 class 개수만큼 SVM 모델이 필요하다. 한 차례 학습이 완료되면 hard negative mining기법을 이용해 재학습한다.

hard negative mining

Hard negative를 그대로 직역하면 hard(어렵다) + negative(아니다)가 되고, ‘아니라고 하기 어렵다’로 해석할 수 있다. 즉, 해당 물체가 ‘아니다’라고 말해야하는데 confidence가 너무 높게 나와 진짜처럼 보이는 결과물(bbox)에 해당한다. 아래 사진은 hard negative mining으로 학습을 한 결과이다.

사람의 얼굴을 탐지하는 모델이 있다고 가정하자. 모델이 얼굴을 탐지하기 때문에 positive는 얼굴이 될 것이고, negative는 배경이 된다. 만약 모델이 얼굴(positive)이라고 탐지했지만, 실제로는 배경(실패)인 경우 False(실패) Positive(얼굴) 오류이다. 위 사진에서 빨간색 박스(bbox)가 FP에 해당한다. hard negative는 원래 negative(배경)이지만 positive(얼굴)라고 잘못 예측한 데이터를 말한다. 따라서 사진에 있는 빨간색 상자들은 전부 hard negative가 된다.

mining은 ‘모은다’는 뜻인데, 결국 hard negative mining은 hard negative를 모은다는 뜻이다. 그리고 hard negative sample를 다시 학습시켜 False Positive 오류에 robust한 모델을 만든다.

Bounding Box Regressor

selective search를 통해 얻은 object들의 bbox위치는 부정확할 수 있다. 따라서 bbox들의 위치를 조정해주기 위해 boundiner box regressor를 사용한다. 먼저 사진으로 이해를 해보자.

이해하기 진짜 어려웠는데, 오늘부로 끝장을 보자!!!!

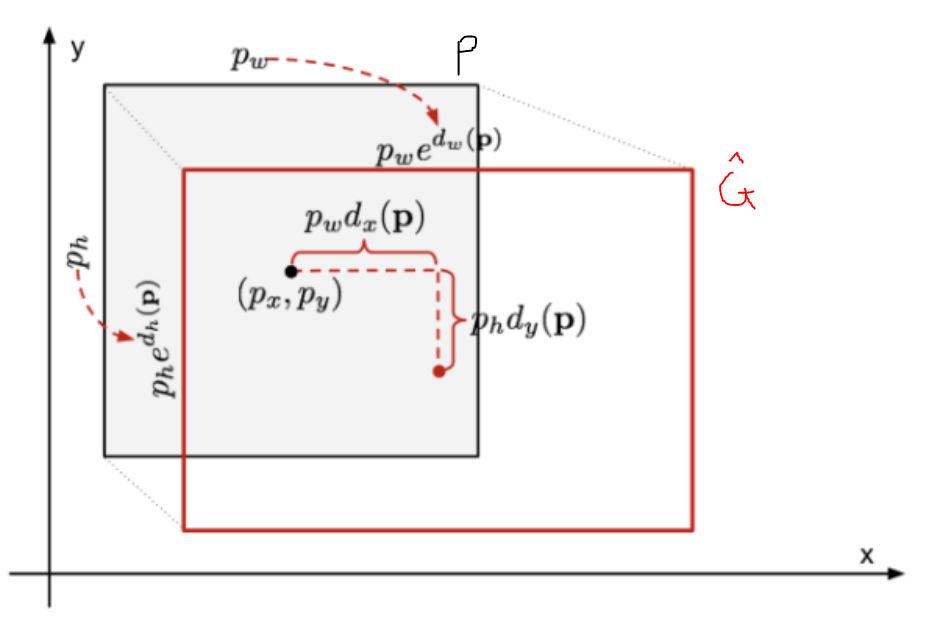
Bounding box regressor의 목표는 예측된 bbox를 정답 bbox로 변환하는 Transformation를 찾는 것이다. 사진에서 검은색 네모가 예측 된 bbox($P$)이고 빨간색 네모가 Transformation된 bbox($\hat{G}$)라고 할 때, Transformation(그림에서는 $d_x, d_y, d_h, d_w$)를 찾는 것이 목표이다. Regressor이기에 회귀식으로 생각하면 $y = wX + b$에서 w가 transformation라고 말할 수 있다. 그러면 transformation을 학습하기 위해서는 정답 transformation과 regressor를 통해 얻은 transformation의 차이가 최소로 하는 transformation을 구해주면 된다.

목표를 알았으니, 이제 본격적으로 수학식을 통해 알아보자.

\[P^i = (P^i_x, P^i_y, P^i_w, P^i_h) \\ \quad \\ G^i = (G^i_x, G^i_y, G^i_w, G^i_h) \\ \quad \\ (x,y) = center, \quad (w,h) = width, hegith\]

N개의 Training Pair ${(P^i, G^i)}_{i=1,…,N}$에 대해서 $P^i = (P^i_x, P^i_y, P^i_w, P^i_h)$는 특정 region의 예측된 bbox좌표값이고 $G^i = (G^i_x, G^i_y, G^i_w, G^i_h)$은 해당 region의 ground truth값이다. 우리는 $P$를 $G$와 유사하게 이동시켜주는 함수(transformation)를 찾는 것이 목표이다.

\[d(P) = [d_x(P), d_y(P), d_w(P), d_h(P)]\]

입력값 $P$에 대해 추정값($\hat{G}$)은 다음과 같이 구할 수 있다. $\hat{G}$는 예측된 bbox가 transformation에 의해 변환된 결과이다.

\[\begin{aligned} & (1) \qquad \hat{G}_x = P_wd_x(P) + P_x \\ & (2) \qquad \hat{G}_y = P_hd_y(P) + P_y \\ & (3) \qquad \hat{G}_w = P{_w}\exp(d_w(P)) \\ & (4) \qquad \hat{G}_h = P{_h}\exp(d_h(P)) \\ \end{aligned}\]

위 식을 $d(P)$에 대한 식으로 바꾸면 다음과 같다.

\[\begin{aligned} & (1) \qquad d_x(P) = (\hat{G}_x - P_x)/P_w \\ & (2) \qquad d_y(P) = (\hat{G}_y - P_y)/P_h \\ & (3) \qquad d_w(P) = \log(\hat{G}_w/P_w) \\ & (4) \qquad d_h(P) = \log(\hat{G}_h/P_h) \end{aligned}\]

$P$와 $[P_x, P_y, P_w, P_h]$는 다른 값이다. $P$는 CNN feature에 있는 Layer 중 $pool_5$의 output(6x6x256)이고, 후자는 모델 초반에 region proposal을 추출했을 때 해당 region의 좌표이다. 적절한 $d()$를 찾아주기 위한 손실함수는 다음과 같다.

\[w_⋆ = \argmin_{\hat{w}_⋆}{\sum^N_i(t^i_⋆ - \hat{w}^T_⋆\phi_5(P^i))^2 + \lambda\lVert \hat{w}_⋆\lVert^2} \\ \quad \\ d_⋆(P) = w_⋆^T\phi_5(P),\quad ⋆ = [x, y, w, h] \\\]

위 식을 통해 정답 transformation인 $t^i_⋆$와 구하고자 하는 transformation인 $\hat{w}^T_⋆\phi_5(P^i)$의 차이를 최소로 하는 $w_⋆$를 구하는 것이 목표가 되었다. $\lambda$는 ridge regression을 위한 상수로 논문에서는 1000을 사용했다고 한다. $d_⋆(P)$에 대한 식은 위에서 구했고, $t^i_⋆$에 대한 식은 $d_⋆(P)$와 동일하지만 추정값($\hat{G}$)를 ground truth값($G$)로만 변경하면 된다.

\[\begin{aligned} & (1) \qquad t_x = (G_x - P_x)/P_w \\ & (2) \qquad t_y = (G_x - P_y)/P_h \\ & (3) \qquad t_w = \log(G_x/P_w) \\ & (4) \qquad t_h = \log(G_x/P_h) \end{aligned}\]

Bounding box regression에 사용되는 $P$는 ground truth와 IoU값이 0.6이상인 region proposal만 사용한다.

Non Maximum Supression

Selective search에 의해 추출된 2000개의 region proposals가 모두 사용된다면 계산량이 많아지고,이미지 내에 특정 object가 있는 부분 주위에 생성되는 겹쳐진 bbox가 많을 것이다. 따라서 겹쳐진 여러 bbox들을 제거하기 위해 Non Maximum Supressoin 알고리즘을 사용한다.

알고리즘은 각 class별로 독립적(for each class independently)으로 적용되고, 동작원리는 다음과 같다.

1. SVMs에 의해 classification이 적용된 region proposals들 중 지정한 confidence값을 넘지 못하는 region proposals들은 제거한다.
2. 생존한 region proposals들을 confidence score를 기준으로 내림차순 정렬을 한다.
3. confidence score가 가장 높은 region proposal를 기준으로 다른 region proposals과 IoU값을 비교하여 특정 threshold값 이상인 region proposals은 모두 제거한다.
4. confidence score가 높은 순서대로 (3) 과정을 반복수행한다.