딥러닝의 학습이 끝나면 해당 모델의 성능을 평가한다. 흔히 생각할 수 있는 평가지표는 ‘모델이 예측한 것 중 실제로 정답과 같은 비율’을 나타내는 정확도(Accuracy) 지표가 있다. 물론 이 지표가 단순하고 직관적이며 구현도 간단하여 충분히 모델의 성능을 대변할 수 있지만, 이 지표만 사용했을 때는 많은 문제가 야기된다.
따라서 이번 포스터에서는 정확도 지표만 사용했을 때의 문제점과 해결방법인 Precision & Recall지표에 대해 알아볼 것이다.
정확도(Accuracy) 한계
보통 모델을 평가할 때 일반적으로 사용하는 평가지표이다. 전체 정답 중 몇 개 맞췄는가?에 대한 답을 도출할 때 사용하는 평가지표이다. 각 물체의 class에 대한 예측률을 평가할 때 사용하는데, Classification을 예로 들면 모델이 강아지로 예측한 전체 개수 중 실제 강아지일 비율을 정량화한 수치이다.
언뜻 보면 Accuracy가 매우 단순하고 구현하기 쉬운 평가지표이고 높으면 무조건 좋은 모델로 착각할 수 있지만, 이 지표 하나로만 모델을 평가하기에는 많은 문제가 있다.
대표적인 예로 강아지 이미지 50장과 고양이 이미지 50장으로 총 100개의 이미지가 있다고 할 때, 모델이 100장 모두 ‘강아지’로 예측했다고 하자. Accuracy를 구하면 50%가 나온다. 물론 절반만 맞췄기 때문에 50%라고 정량적으로 말할 수 있지만, 만약 모델이 학습에 의해 예측한 것이 아닌 무조건 ‘강아지’로만 예측을 하는 모델이라고 생각해보자. 이런 모델이 과연 50%정도의 정확도를 가진 모델이라고 할 수 있을까? 이런 문제는 데이터셋이 불균형한 상황(Class-Imbalanced Dataset)일 때 두드러지게 나타난다. 총 100장의 사진 중 강아지만 80장이 있고 나머지 20장은 어떠한 class가 있든간에 무조건 ‘강아지’로만 예측하는 모델의 경우 항상 80%의 정확도를 보이는 문제가 있다.
이러한 문제점을 해결하고 모델을 좀 더 정확히 평가하기 위해 사용하는 지표가 바로 Precision과 Recall이다.
Precision & Recall
보통 정밀도(Precision)와 재현율(Recall, Sensitivity)라고 불리는 이 지표는 모델을 Accuracy로만 평가했을 때 발생할 수 있는 문제를 해결해준다. 이 지표를 이해하기 위해서 아래 표를 참고하면 매우 간단하다.
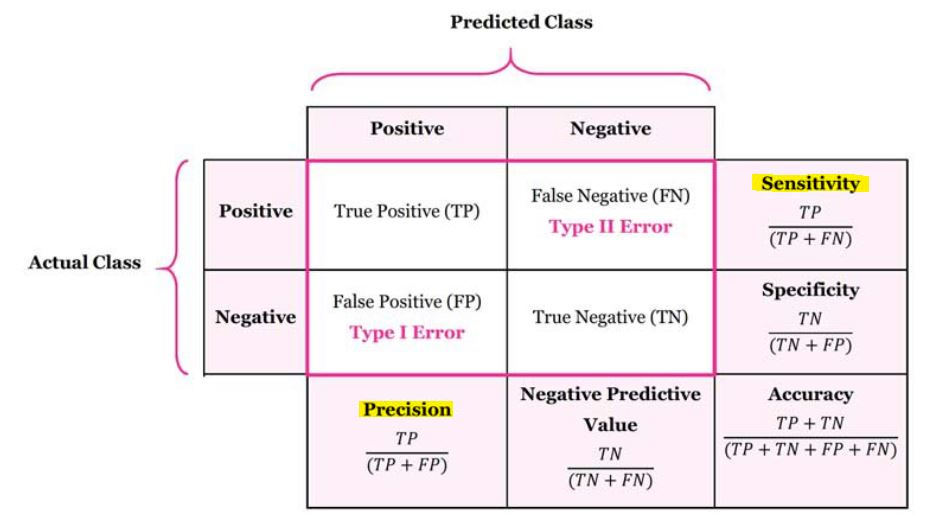
Precision과 Recall의 관계를 볼 때는 '평가를 할 때는 2개의 데이터를 비교한다.'라는 전제를 잘 생각하고 있어야 한다. 하나는 정답 레이블, 다른 하나는 모델이 예측한 결과이다. 모델이 예측한 결과를 정답과 비교해서 해당 예측을 다음과 같이 4가지 경우 중 1개의 경우로 치환하는 것이다.
- TP(True Positive) : 강아지라고 예측한 것 중 실제로 강아지인 경우
- FP(False Positive) : 강아지라고 예측한 것 중 실제로 강아지가 아닌 경우
- FN(False Negative) : 강이지가 아니라고 예측한 것 중 실제로 강아지인 경우
- TN(True Negative) : 강아지가 아니라고 예측한 것 중 실제로 강아지가 아닌 경우
여기서 언급되는 Positive와 Negative는 긍정, 부정의 뜻이 아니라 모델이 특정 class를 class라고 예측을 했냐 안 했냐의 차이이다.
Precision
Precision의 경우 모델이 ‘강아지’라고 예측한 것들 중 정답과 비교했을 때 실제로 강아지인 비율을 말한다. 이 경우에는 모델이 ‘강아지가 아니다라고 예측한 경우’는 고려하지 않는다. 따라서 Precision의 식은 다음과 같다.
Recall
Recall의 경우 모델이 예측한 모든 결과(강아지가 맞다, 아니다 모두) 중 정답과 비교했을 때 실제로 강아지로 잘 예측한 비율이다. 이 경우는 ‘실제 강아지가 아닌 경우’와의 비교는 고려하지 않는다. 따라서 Recall의 식은 다음과 같다.
Precision과 Recall의 식을 보면 둘 다 True Positive가 공통분자로 포함되어 있다. 이 말은 곧 ‘실제 강아지’를 ‘강아지가 맞다’고 예측한 수가 많으면 값이 커진다는 뜻이다. 하지만 서로 다른 결과(FP, FN)에 따라 값이 차이가 난다. 따라서 Accuracy가 100%이 아닌 이상은 Precision과 Recall의 관계는 반비례 관계가 된다. 예를 들어 정확도는 같은데 Precision의 수치를 높이기 위해 FP을 줄이면, 그 만큼 FN은 늘어나기 때문이다.
위에서는 ‘강아지 판별’을 예시로 사용했는데, 좀 더 명확하게 하기 위해서는 ‘암 검출’ 모델을 예시로 사용하면 된다. 암 검출에서 Recall의 경우 실제로 암을 가지고 있는 환자에 대해 암으로 예측할 확률을 나타내는데, 이 수치를 높이기 위해 모델이 암으로 진단할 경우의 수를 늘리면 TP가 증가할 순 있지만 반대로 FP또한 증가하기 때문에 Precision값은 작아진다.
그렇다면 어떤 상황에서 무슨 지표가 높아야하는걸까?
위에 언급한 암 검출을 예시로 들면, 실제로 ‘암이 있는 환자’에게서 ‘암이 있다’고 진단을 내려야 하는데, 만약 ‘암이 없다’고 진단을 내리면 매우 위험한 상황이 발생한다. 하지만 반대로 ‘암이 없는 환자’에게 ‘암이 있다’고 진단을 내리는 경우 놀랄 수는 있어도 단순 헤프닝으로 끝날 수 있다.(물론 이런 경우도 옳지는 않지만, 둘 중 하나만 발생해야한다면 후자의 경우가 더 낫다는 뜻이다.) 따라서 암을 검출하는 모델의 경우 Recall의 수치가 높아야한다. 무조건 다 암이라고 예측하면 암이 아닌 환자에게 암이라고 진단을 내릴 순 있어도 최소한 진짜 환자를 놓치는 경우는 없기 때문이다.
반대로 죄의 유무를 판별하는 모델이 있다고 생각해보자. ‘100명의 죄인을 놓치더라도 한 사람의 무고한 사람을 처벌하지 말라’는 무죄추정의 원칙을 적용하면 실제로 죄를 짓지 않은 사람에게 죄가 있다고 예측하는 경우(FP)가 낮아야하기 때문에 Recall 보다는 Precision이 높아야 한다.
이처럼 현재 해결하고자 하는 문제가 무엇이냐에 따라 적당한 지표를 선정해서 해당 지표의 수치를 올리는 방향으로 모델을 설계해야한다.
F1 Score
Precision과 Recall의 수치로 모델을 평가하면 비교적 객관적으로 해당 모델의 성능을 대변할 수 있을 것이다. 하지만 대부분의 결정권자?들은 이런식으로 나눠져 있으면 복잡하기 때문에 ‘그래서 그 모델이 좋다는거야?’ 등의 의문에 쉽게 정답을 도출해내지 못하는 경우가 많다. 따라서 두 지표를 한 가지 지표로 표현하기 위해 새로운 지표를 만들었는데, 그것이 F1 Score이다.
F1 Score는 간단히 두 지표(Precision, Recall)의 조화평균으로 나타낼 수 있다.
F1 Score의 장점으로는 한 가지 지표로 대체할 수 있다는 점과 **Class가 불균형한 데이터(Class Imbalance Dataset)일 때 정확하게 성능을 평가할 수 있다. 그 이유는 산술평균이 아닌 조화평균을 사용함으로서 비중이 큰 bias의 영향이 줄어들어 불균형한 문제를 보정하기 때문이다.
지금까지 Precision과 Recall, F1 Score에 대해 알아보았다. 단순히 정확도로만 모델을 평가하면 매우 위험하다는 것을 알 수 있었다. 그리고 추후에 Precision-Recall Curve와 같은 지표로도 확장이 가능하기 때문에 개념을 정확하게 숙지하고 있어야 할 것 같다.