오늘은 과적합을 방지하는 테크닉 중 하나인 Drop Out에 대해 알아보도록 하자.
Deep Learning의 문제점
과적합(Overfitting)
과적합이란 모델이 학습 데이터에 대해서만 지나치게 학습한 나머지 일반화되지 못해서 실제 데이터에서는 Loss값이 감소하지 않고 좋은 성능을 보이지 못 하는 현상을 말한다. 여기를 참고하면 자세히 알 수 있듯이 ‘Training Datasets에 대해서만 매우 적합한 모델이 된 상태’를 말한다.
과적합이 발생하는 이유는 다양하지만, 대표적으로 다음과 같다.
- 학습 데이터에 노이즈가 많은 경우
- 모델이 너무 복잡할 때(파라미터의 수가 많을 때)
- 학습하는 데이터가 매우 부족할 떄
Co-adaptation(동조현상)
인공신경망 구조의 본질적인 이슈중 하나로 Co-adaptation가 있다. 모델을 학습시킬 때 학습 데이터에 의해 weight들이 서로 동조화되는 현상이다. 즉,weights들이 다른 weight에 의존하게 되면서 서로 영향을 주는 현상을 말한다.
- 특정 Weight가 너무 커버리면 다른 weight들의 영향이 상대적으로 적어진다.
- 비슷한 feature를 detect하는 뉴런이 발생하면 결국 computation 낭비로 이어진다.
따라서 각 뉴런들이 독립적으로 feature를 추출할 수 있도록 분리해줄 필요가 있다.
Drop Out
위에서 언급한 2가지 문제를 해결하기 위해 Drop Out 방법이 제시되었다.(물론 Ensemble효과도 있지만, 이건 얻어지는 ‘효과’에서 다루기로 하겠다.) Drop Out이란 모델의 일부 네트워크를 생략하는 것을 말한다. 네트워크 속 노드를 강제로 랜덤하게 0값으로 만들어서 해당 노드가 학습에 참여하지 않도록 한다.
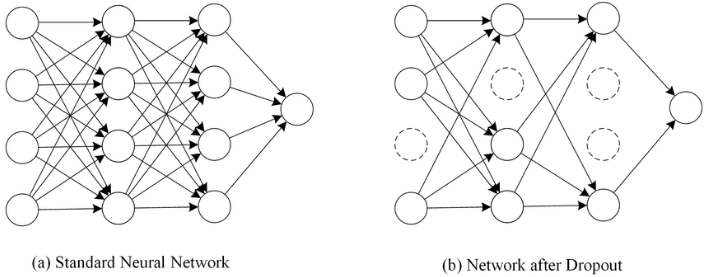
Drop Out을 적용할 때는 확률값($p$)를 이용한다. ‘각 뉴런이 생략되지 않을 확률($p$)’을 이용해 뉴런의 생사를 결정한다. 모델이 학습을 할 때 $p$값에 의해 뉴런이 랜덤적으로 0값이 되고, 결과적으로 매 학습마다 다른 모델을 학습하는 것과 같아진다. 이 현상은 결국 Ensemble(앙상블)효과를 야기시킨다.
Drop Out의 효과
위에서 언급했듯이 각 뉴런들이 동조화 되는 Co-adaptation를 방지하는 효과가 있다. 보통의 신경망에서는 weight들이 서로 연결되어있고 한 뉴런으로 모이면서 각자가 어떤 영향을 주는지 알고 있는 상태이다. 따라서 loss를 갱신할 때 서로에게 영향을 준다. Drop out을 통해 학습을 하는 동안, 서로 영향을 주던 weight들의 관례를 break함으로서 각 뉴런들이 독립적으로 feature를 추출할 수 있도록 해준다.

보통 신경망에서 모델을 결합(Ensemble)하면 학습의 성능을 개선할 수 있다. 서로 다른 구조의 모델을 학습을 하는 경우를 말한다. 하지만 신경망이 깊어질수록 여러개의 모델을 학습하는 것은 무리가 있다. Drop Out은 이러한 문제를 해결하는 동시에 모델 결합(Model Combination) 효과를 야기한다.
Drop Out 기법으로 인해 랜덤으로 뉴런을 생략하면 투표호과(voting)를 내면서 학습을 진행하게 된다. 즉, 생략된 뉴런이 매 학습마다 다양하기 때문에 마치 다른 모델을 학습한 것 같은 효과를 준다. 상대적으로 ‘thin’ 한 여러 네트워크를 샘플링하여 모델을 test할 때 예측값을 평균내는 효과를 내서 과적합을 방지하고 Regularization 효과를 준다.
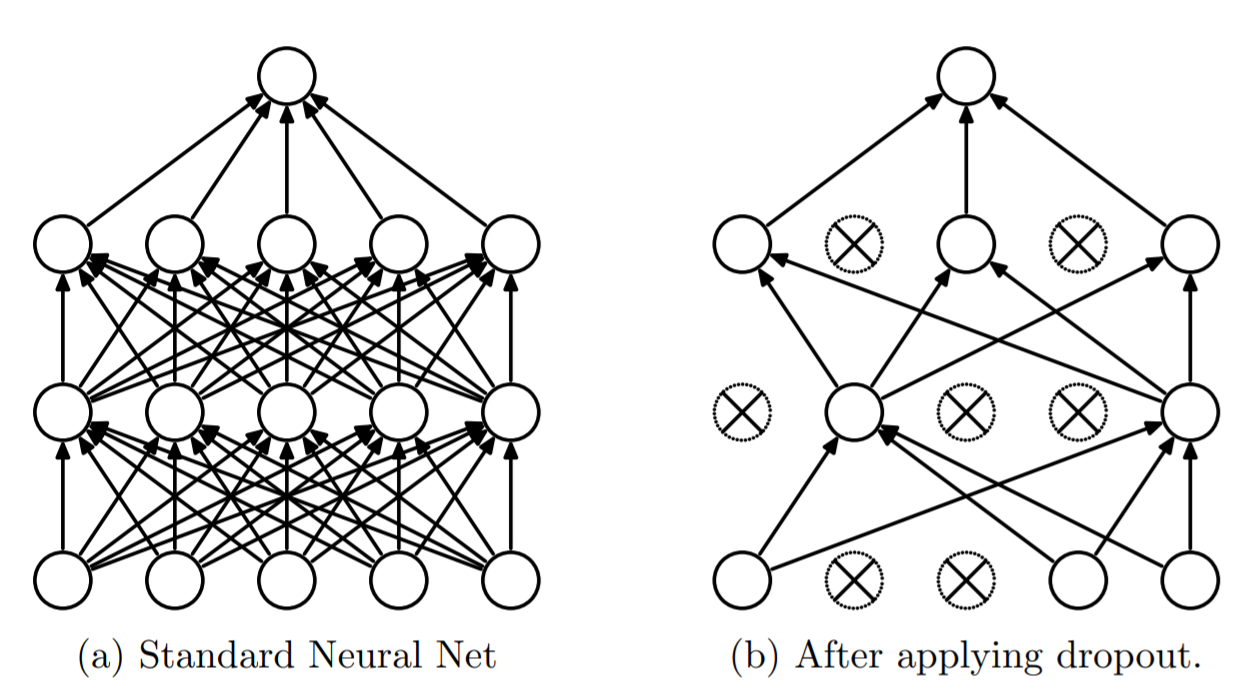
Drop Out이 Co-adaptation을 방지하는 더 직관적인 이유
포스터에서 자주 말했듯이 필자는 많이 멍청해서 ‘쉽게 설명된 것’을 찾아다니느라 애를 쓴다. “Dropout: A Simple Way to Prevent Neural Networks from Overfitting”라는 논문에 이런 표현이 있었다.
Drop out은 가끔씩 뉴런들을 없애서 평소에는 서로 영향을 주던 뉴런들이 ‘없는 상태’에서 loss값을 감소시켜야 한다. 즉, 서로를 신뢰하지 못하도록 만든다. 따라서 결과적으로 각 뉴런들은 각자 독립성을 키울 수 있게 된다.
원본은 다음과 같다.(나름대로 MSG를 첨가해서 필자만의 언어로 해석했습니다.)
We hypothesize that for each hidden unit, dropout prevents co-adaptation by making the presence of other hidden units unreliable. Therefore, a hidden unit cannot rely on other specific units to correct its mistakes. It must perform well in a wide variety of different contexts provided by the other hidden units. To observe this effect directly, we look at the first level features learned by neural networks trained on visual tasks with and without dropout.
Drop out이 적용되는 방식
Drop Out은 Training을 할 때 적용이 된다. 생략되지 않을 확률($p$)에 따라 학습 간에 뉴런이 생략이 된다. 이후에 Test를 하게 되면 $p$가 적용됐던 뉴런에서 나가는 Weight값에 대해 각각 $p$값을 곱해준다. 각 Weight들은 $p$확률로 출현하기 때문에 곱해주는 것이다.

논문에 있는 사진들을 참고했을 때 이해가 더 어려웠다. Dropout은 신경망 안에 있는 ‘노드’에 영향을 주는 기법이지, weight와는 아무 상관이 없다. 근데 자꾸 weight랑 엮을라고 하니까 이해가 너무 어려웠다. 사진(3)을 보면 ‘weight’값에 $p$를 곱했는데, 사실 이건 그냥 ‘노드’에다가 $p$값을 곱한 것과 같다.
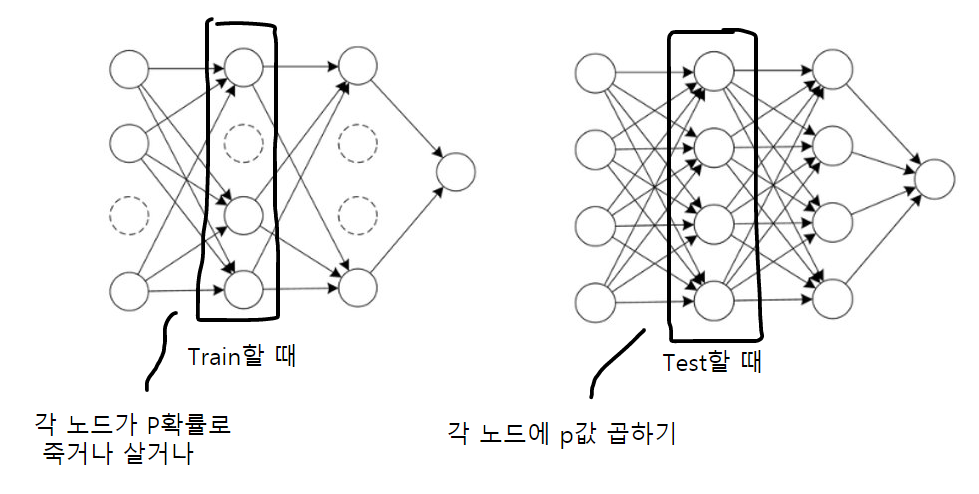
위 사진과 같이 ‘노드’에만 신경을 쓰면 된다. 식으로 보면 다음과 같다.

위 식에서 ‘Dropout Network’ 부분에 있는 $y^{(l)}$는 직전 layer에서 나온 ‘노드’이고 그 노드값에 0또는 1값인 $r^{(l)}$을 곱해서 노드의 생,사를 결정한다.($r^{(l)}$은 0또는 1이고, Bernoulli 확률값 $p$에 따라 0또는 1이 결정된다.)
Pytorch로 실습하기
Dropout을 적용하는 방법은 다음과 같다.
import torch
import torch.nn as nn
class mymodel(nn.Module):
def __init__(self):
super(mymodel, self).__init__()
self.fc1 = nn.Linear(5,4)
self.fc2 = nn.Linear(4,3)
self.fc3 = nn.Linear(3,2)
self.dropout = nn.Dropout(p=0.5) # Dropout instance 설정(0.5확률)
def forward(self, x):
x1 = self.fc1(x)
x2 = self.dropout(x1) # fc2까지 계산 된 결과에 dropout 적용(x가 노드이기 때문에~)
x3 = self.fc2(x2)
x4 = self.fc3(x3)
return x4
nn.Dropout(p=0.5): 0.5의 확률로 Dropout 적용
아래 사진은 위 코드에 대한 네트워크이다.

각 노드가 50%확률로 살아있는거지 전체 갯수 중에 50%만 살아남는 것이 아니다. 위 식의 각 노드값을 보면 다음과 같다.
# input(==x) ===== tensor([1., 1., 1., 1., 1.])
# x1 ===== tensor([-0.2021, -0.8614, -0.1749, -0.6106], grad_fn=<AddBackward0>)
# drop ==== tensor([-0.4041, -0.0000, -0.0000, -0.0000], grad_fn=<MulBackward0>)
# x2 ===== tensor([ 0.6346, -0.1302, -0.0872], grad_fn=<AddBackward0>)
# x3 ===== tensor([0.5077, 0.5231], grad_fn=<AddBackward0>)
Pytorch에서 Dropout의 특징(Scaling)
Pytorch에서 제공하는 Dropout에 대한 설명을 보면 다음과 같은 내용이 있다.
Furthermore, the outputs are scaled by a factor of $\frac{1}{1-p}$ during training. This means that during evaluation the module simply computes an identity function.
Train을 할 때 dropout을 적용하면 각 노드들이 $\frac{1}{1-p}$값이 곱해진다는 뜻이다. 갑자기 이 식은 어디서 나온 것일까?
위 글에서도 언급을 했지만 train할 때 p확률로 노드가 off되었으니, test를 할 때는 (1-p)확률로 노드가 on될 것이다. test할 때는 모든 노드가 정상적으로 작동해야하기에 dropout이 적용되는 노드(Layer)에 (1-p)확률을 곱해줘야한다.
그런데 dropout은 train일 때만 단지 노드들을 0값으로 만들어서 마치 그 노드가 train에 참여하지 않는 것 처럼 보이게 만들려는 것일 뿐, test 모드일 때는 모든 수치가 처음 모델과 같아야하기 때문에 (1-p)가 곱해져도 처음 모델과 같도록 조치를 해줘야하고, 따라서 train일 때 $\frac{1}{1-p}$로 scaling되는 것이다.
따라서 실제 코드를 보면 train과 eval 모드일 때 각각의 dropout의 결과가 다르다.
(위 코드에서 결과만 가져오면)
model.train()
model(a)
# x1 ===== tensor([ 0.6792, 0.0767, -0.1639, -0.4744], grad_fn=<AddBackward0>)
# drop ==== tensor([ 0.0000, 0.1535, -0.3277, -0.0000], grad_fn=<MulBackward0>)
model.eval()
model(a)
# x1 ===== tensor([ 0.6792, 0.0767, -0.1639, -0.4744], grad_fn=<AddBackward0>)
# drop ==== tensor([ 0.6792, 0.0767, -0.1639, -0.4744], grad_fn=<AddBackward0>)
- train모드에서는 x1이 scaling되어 값이 다르게 보이고(노드가 0값으로 바뀌지 않은 노드 참고)
- test모드에서는 x1과 dropout에서의 노드값이 똑같이 나온다.
Docu에서 scaling에 대한 내용을 봤을 때 혼란스러웠는데, 역시나 이러한 이유가 숨어져있었다.
또한 논문에서는 p가 살아남을 확률, Python Document에서는 p가 죽을 확률을 나타냅니다. 헷깔리지 않도록 주의!
지금까지 Dropout에 대해 알아보았다. 논문에 나온 그림들을 보고 참고했을 때는 이해가 어려웠는데, ‘노드’에만 신경을 쓴다고 생각하면 이해가 쉬웠다. ‘weight’에다가 하는 것은 Dropconnect라는 다른 기법이 있다. 기회가 된다면 dropconnect도 한 번 다뤄보도록 하겠다.