이번 포스터에서는 모델의 과적합을 방지하는 테크닉 중 하나인 정규화(Regularization)에 대해 알아보도록 하자.
과적합
대부분의 테크닉들이 모두 과적합을 방지하기 위해 만들어진 것 같다. 뭐만 하면 과적합을 막을 수 있다고 하니까….
과적합이란 학습 데이터만 지나치게 학습한 나머지 모델이 일반화되지 못 해서 새로운 데이터에 대해 예측을 잘 하지 못 하는 상태를 말한다. 학습할 때는 Loss가 감소하지만, 실제 Test에 대해서는 Loss가 감소하지 않는 현상을 보인다. “Training Datasets에 대해서만 매우 적합한 모델’이 된 셈이다. 과적합에 대한 자세한 내용은 여기에서 볼 수 있다.
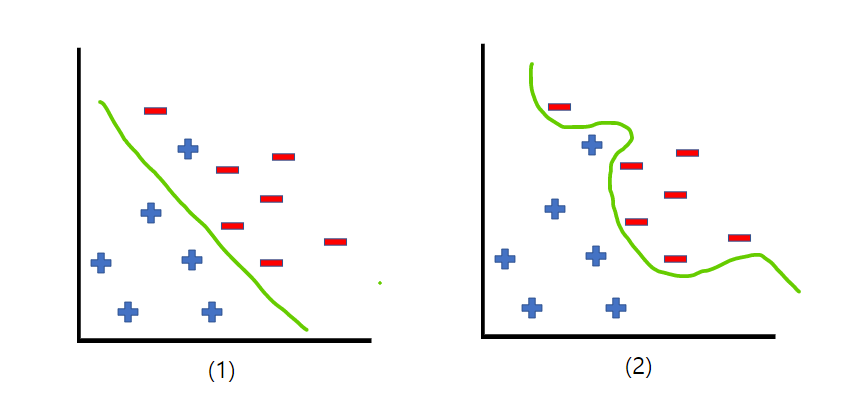
위 사진을 보면 ‘정확도’를 기준으로 판단을 한다면 당연히 (2)가 좋아보인다. 하지만 보통 (2)처럼 학습이 된 모델에 새로운 데이터를 입력하게 되면 예측을 잘 하지 못 하는 경우가 더 많다. 그 이유는 현재 가지고 있는 학습 데이터에 대해서만 학습이 되어버렸기 때문이다. 따라서 (2)와 같은 모델을 (1)과 같이 일반화를 해 줄 필요가 있다. 이와 같은 문제를 해결하기 위해 정규화(Regularization)를 이용한다.
정규화(Regularization)
정규화(Regularization)은 보통 ‘일반화’라고 번역되기도 하는데, 모델에 ‘제약’을 걸어서 모델의 복잡도(Complexity)를 줄여 일반화(Generalization)를 개선하는 기법을 말한다. weight값에 패널티를 가해서 과도하게 커지는 것을 방지한다.
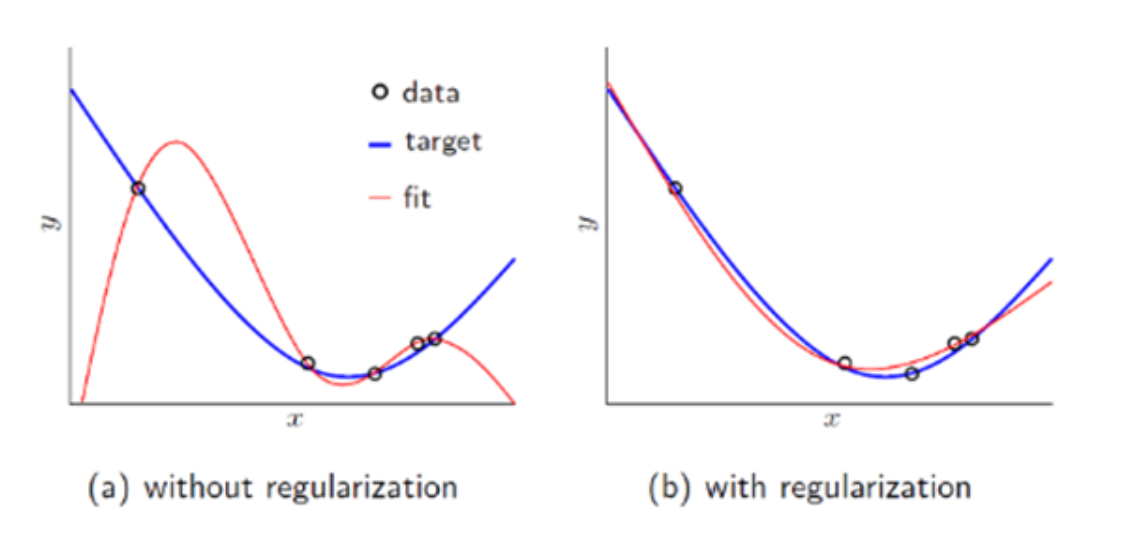
기계학습을 하는 과정에서 모델이 ‘학습’을 한다는 것은 weight을 조정하는 것, 다시 말해 손실(Loss)을 줄이는 방향으로 Weight을 갱신하는 것을 말한다. 학습 데이터를 이용해 단순히 Loss가 최소가 되는 방향으로 진행을 하다 보면, 특정 weight값이 다른 weight에 비해 상대적으로 커지면서 모델의 성능을 악화시키는 경우가 있다. 모델의 복잡도가 증가해서 과적합이 발생한다. 따라서 Loss를 감소시키는 동시에 Regularization을 통해 weight값이 커지지 않도록 제약을 걸어줘야한다.
아래 사진을 참고하면 위 설명을 직관적으로 이해할 수 있다.
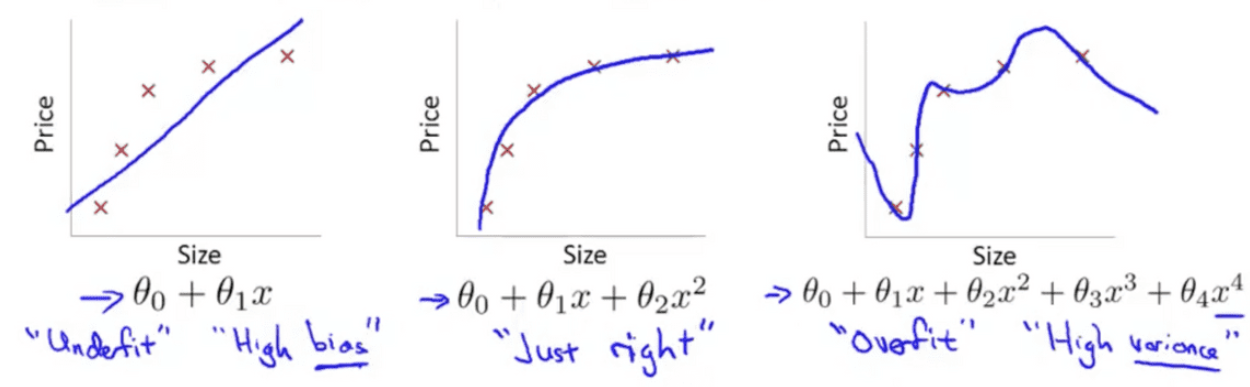
Regularization을 통해 $\theta$값에 제약을 걸어줘서 모델이 복잡해지는 현상을 막을 수 있다.
결론적으로 Regularization은 모델의 Generalization을 개선하는 기법
Regularization 수학적 표현
필자는 Regularization을 하는 방법 중에 ‘weight decay’ 기법을 소개할 것이다. 해석하면 ‘가중치 감소’를 의미한다. weight값을 감소시켜 결과적으로 모델의 복잡도(Complexity)을 감소시키는 방법이다. 수학적 표현은 다음과 같다.(L2 Regularization 예시)
- $J(\theta)$ : 모델의 목적함수(objective Function)
- $J_0(\theta)$ : 손실함수(Loss Function)
- $\lambda$ : weight에 제약을 가하는 정도
- $\theta$ : 가중치(weight)
위에서 ‘목적함수’라는 표현을 사용했는데, 보통 손실함수(MSE, CEE 등)와 혼용해서 사용하기도 한다. 하지만 여기서는 Regulariazation이 포함된 손실함수이기 떄문에 두 개를 합친 것을 표현하기 위해 목적함수라고 칭했다. 최종적으로 모델은 목적함수가 최소가 되도록 학습을 한다.
딥러닝을 학습할 때 주로 사용하는 방법 중 하나인 경사하강법(Gradient Descent)을 적용하고 손실함수로는 MSE를 사용했을 때 weight가 갱신되는 식은 다음과 같다.
위 식에서 알 수 있듯이 가중치($\theta_i$)에 $(1-\eta\frac{\lambda}{n})$을 곱해주기 때문에 weight값이 작아지는 방향으로 학습을 진행한다. 이와 같이 weight값이 작아지도록 학습을 하는 방식이 weight decay라고 한다. weight decay기법으로 인해 비정상적으로 커지는 weight값을 방지할 수 있다. weight값을 작아지도록 한다는 것은 곧 학습에서 ‘local noise’의 영향을 최소화한다는 것을 의미한다. 최종적으로 일반화(Generalization)을 개선하는 것이다.
Regularization 종류
가장 대표적으로 L1, L2 Regularization이 있다. 정규화식은 보통 손실함수 뒤에 추가로 붙는 식이기 때문에 다음과 같이 표현할 수 있다.
L2 Regularization(Ridge)
릿지라고도 불리며, 위에서 예시로 언급했던 식이 바로 L2 Regularization이다. 공식은 다음과 같다.
n: 데이터의 개수- $\lambda$ : 하이퍼 파라미터
기존 경사하강법 식에서 $(1-\eta\frac{\lambda}{n})$이 추가되었기 때문에 가중치값이 일정 비율로 감소한다. L2의 경우 Weight의 크기에 따라 제약이 되는 정도가 달라진다. $\theta$값이 크면 더 크게, 작으면 더 작게 갱신을 한다.
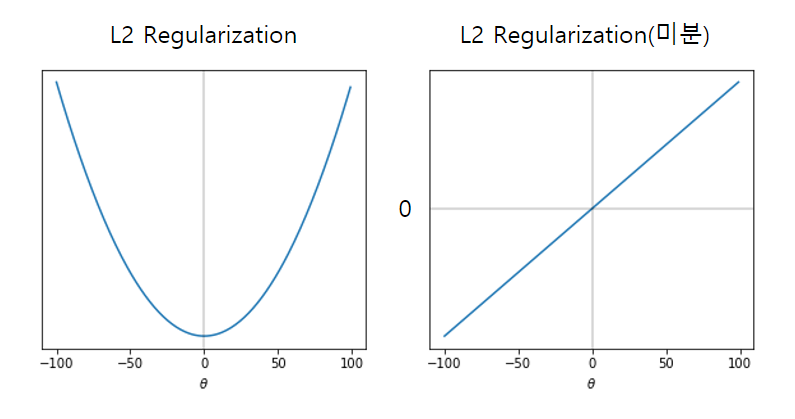
L2 Regularization을 미분하면 다음과 같은 그래프가 그려진다.
L1 Regularization(Lasso)
랏쏘라고도 불리며, L2와 비슷하지만 젭고이 아닌 절대값을 사용한다.
n: 데이터의 개수- $\lambda$ : 하이퍼 파라미터
- sgn($\theta$) : 부호 함수(1 또는 -1 또는 0)
위 식에서 sgn()은 부호 함수로, weight에 따라 1또는 -1(또는 0)값이 설정된다. 따라서 L2와 다르게 L1은 일정한 상수만큼 weight이 변화한다. 또한 L2에는 분모에 2가 있는데, 이것은 단순히 미분을 할 때 편리하게 하려고 사용한 상수이다.
L1을 미분하면 다음과 같은 그래프가 그려진다.
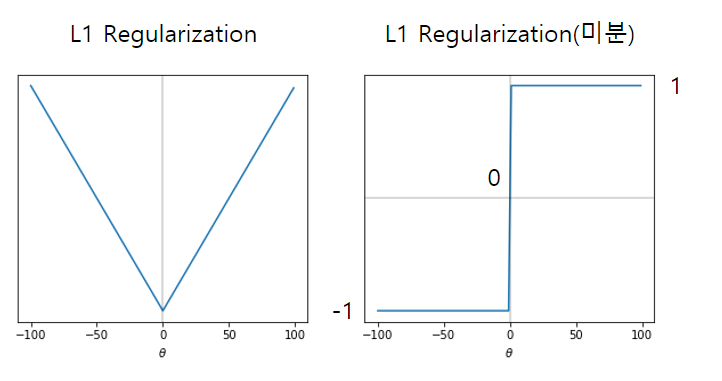
Elastic Net(엘라스틱넷)
엘라스틱넷은 L1과 L2를 합친 버젼을 말한다. L1과 L2의 최적화 지점이 서로 다르기 때문에 두 정규화 항을 합친 후 r값으로 각각의 규제 정도를 조절한다.
식에서도 알 수 있듯이 r값이 0이면 L2, 1이면 L1이 된다.
각각을 언제 사용해야하나?
우선 규제가 약간 있는 것이 없는 것보다는 일반적으로 매우 좋기 때문에 Regularization을 사용하는 것이 좋다. 대부분은 L2가 기본이 되지만 사용하는 특성(feature)가 몇 개 뿐이라고 판단되면 L1아니 엘라스틱넷을 사용하는 것이 더 좋다.(불필요한 특성을 0값으로 만들어주기 때문에)
L1과 L2의 비교
Robustness(L1 > L2)
통계학에서 Robust하다는 것은 ‘이상치/에러값으로부터 영향을 크게 받지 않는다’라는 뜻이다. 즉, Robustness가 크면 이상치에 대한 저항값이 크다는 말이다. 따라서 데이터를 학습하는데 있어서 ‘이상치’에 관심이 없다면(있으나 마나 노상관) L1 Regularization을 사용하는 것이 좋다.
- L2의 경우 weight값을 제곱하기 떄문에 L1보다 비교적 큰 수치로 작용한다.
Stability(L1 < L2)
Stabilty란 ‘비슷한 데이터에 대해 얼마나 일관적으로 예측할 수 있는가’에 대한 지표인다. L1과 L2의 미분 그래프를 보면 다음과 같다.
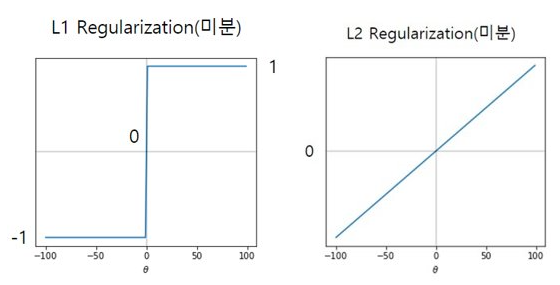
L1의 경우 1또는 -1로 정해져서 일정한 상수값으로 weight가 감소하는 반면, L2의 경우 weight의 값에 비례해서 감소한다. L2가 weight값에 영향을 많아 Minimum 근처에서 상대적으로 변화가 더 적을 수 밖에 없다. 따라서 L2가 L1보다 변화에 더 안정적이라고 할 수 있다.(weight가 매우 크면??)
Sparsity
모델이 학습을 하면서 각 파라미터들의 연관성(가중치값)을 계산하게 된다. 그 중에 연관성이 매우 낮은 파라미터들은 0에 가까운 숫자로 만드는 것이 좋은 모델을 만드는 것과 같다.(복잡도가 낮아짐) 실제로 L1 Regularization을 사용하면 weight가 0값으로 만들어지는 경우가 있다. 그 이유는 위에서 언급했듯이 L1은 일정한 상수값을 이용해 weight을 감소시키기 때문이다. 따라서 L2보다 L1이 더 Sparsity한 모델을 만드는데 유리하다.
이와 같은 특징(weight을 0으로 만듦)은 결국 Feature Selection으로도 이어질 수 있다. 다음과 같이 두 벡터가 있다고 하자.
두 벡터를 L1으로 구하면
두 벡터를 L2로 구하면
\[\begin{aligned} ||a||_2 & = \sqrt{0.25^2 + 0.25^2 + 0.25^2 + 0.25^2} = 0.5 \\ ||b||_2 & = \sqrt{(-0.5)^2 + 0^2 + (0.5)^2 + 0^2} = 0.707 \end{aligned}\]
L1으로 구할 때는 0값이 있음에도 불구하고 똑같이 1이라는 결과가 나오지만(즉, 같은 결과를 내는데 다양한 방법이 있다.) L2의 경우에는 각각에 대해 유니크한 결과를 낸다. 즉, L1의 경우에는 특정 vector를 0으로 만들어주어도 같은 값을 낼 수 있다는 뜻이다.
이와 같은 결과가 결국 Feature Selection기능을 할 수 있도록 해준다. 특정 feature들을 0값으로 만들어버리면 나머지 값들로 인해 feature가 select된다고 볼 수 있고 가중치값들이 Sparse한 형태를 가질 수 있다.
가중치 변화도
L1과 L2의 큰 차이 중 하나가 weight의 변화도인데, 아래 그림을 보면 바로 이해할 수 있다.
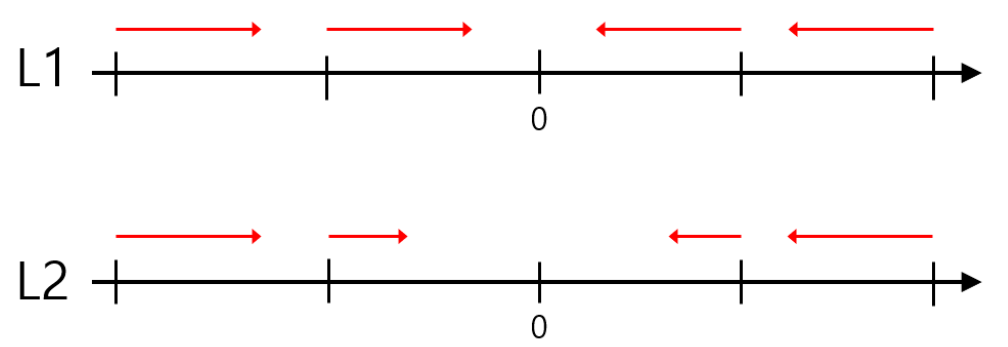
L1과 L2 모두 Regularization을 위해 $\theta$값을 0으로 수렴시키고자 한다. 하지만 L1의 경우 정해진 상수값에 의해 일정하게 감소하는 반면 L2는 weight에 비례해서 감소한다. 따라서 위 사진과 같은 변화도를 가지게 된다.
Pytorch 활용
Pytorch에서 기본적으로 제공하는 Regularization은 L2 뿐이다. 사실 L2가 가장 많이 사용되기 때문에 L2만 구현해놓은게 아닐까 싶다. 하지만 여기서는 L1까지 적용하는 방법에 대해 알아보도록 하겠다. Pytorch 코드 풀버젼은 여기에서 볼 수 있다.
L2 Regularization
최적홤 함수를 정의할 때 사용한 nn.optim을 이용하면 쉽고 빠르게 L2를 구현할 수 있다.
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=0.001)
>>> print(optimizer)
# SGD (
# Parameter Group 0
# dampening: 0
# lr: 0.01
# momentum: 0
# nesterov: False
# weight_decay: 0.001
# )
weight_decay: L2로 설정되어 있고, 입력한 값은 $\lambda$에 해당한다.
L1 Regularization
Pytorch에서는 L1을 따로 제공하지 않는다. 따라서 L1을 사용하고 싶다면 직업 구현을 한 후에 train을 하는 과정에 추가해주면 된다. L1의 식을 다시 한 번 보면 다음과 같다.
위 식을 참고해서 구현하면 다음과 같다.
model = mymodel()
L1_Loss = 0
for param in model.parameters():
L1_Loss = L1_Loss + torch.sum(abs(param))
>>> print(L1_Loss)
# tensor(20.5460, grad_fn=<AddBackward0>)
model.parameters(): 각 layer들의 파라미터들을 호출한다.abs(): 절대값을 계산
위 코드를 Training하는 과정에 추가하면 최종적으로 손실함수를 구할 수 있다.
import torch
import torch.nn as nn
import torch.optim as optim
model = mymodel()
optimizer = optim.SGD(model.parameters(), lr=0.001)
loss_func = nn.MSELoss()
EPOCH = 10
for e in range(1, EPOCH+1):
model.train()
running_loss = 0
for i, data in enumerate(trainloader):
images, labels = data
optimizer.zero_grad()
outputs = model(images)
MSE_Loss = loss_func(outputs, labels) # MSE loss
L1_Loss = 0 # L1 Loss
for param in model.parameters():
L1_loss += torch.sum(abs(param))
Loss = MSE_Loss + a * L1_Loss # a == Lambda값
Loss.backward()
optimizer.step()
running_loss += Loss
now = time.time()
print('\r[%d/%d]-----[%d/%d] LOSS : %.3f' %(e, EPOCH, i, 60000/128), end = '')
print('\n')
지금까지 Regularization에 대해 알아보았다. Pytorch에서도 L2 Regularization 이외에는 제공하지 않을 정도로 나머지 2개는 잘 사용하지 않는 것 같다. 확실히 과적합을 방지하는 기법 중 가장 좋은 방법이라고 생각이 든다.