이전 포스터에서는 Tensor와 Autograd등에 대해 알아보았다. 이번 포스터에서는 Pytorch을 이용해 간단한 연산을 하는 방법에 대해 알아보고 선형회귀를 코드로 구현을 해서 어떤 원리가 적용되고 있는지, 또한 실제로 간단한 데이터를 생성하여 모델을 학습시켜 데이터에 맞는 적절한 모델을 찾는 실습을 해보기로 하자.
선형 회귀(Linear Regression)
일반적으로 사람 키와 몸무게는 서로 상관관계가 있다. 보통 키가 크면 몸무게도 많이 나갈 수 밖에 없다는 것을 잘 알고 있다. 물론 모든 사람에게 똑같이 적용되진 않지만, 선형회귀를 이해하기 위해 키와 몸무게의 관계가 비례관계에 있다고 가정을 해보자!
| 몸무게(kg) | 키(cm) |
|---|---|
| 83 | 180 |
| 93 | 190 |
| 78 | 175 |
| 69 | 166 |
| 56 | 153 |
위 데이터를 통해 간단한 식을 설정하면 다음과 같다.
이 모델은 입력 특성인 키(cm) 에 대한 선형 함수이고 $\theta_0$과 $\theta_1$은 모델의 파라미터이다. 이처럼 키와 몸무게로 얻은 관계식을 ‘선형회귀모델’이라고 부른다. 이 식을 일반화하면 다음과 같다.
위 식에서 $x_n$은 독립변수이며 $\theta_n$은 각 독립변수의 계수, $y$는 종속변수를 의미한다. 쉽게 x가 데이터(키)가 되고, y는 그에 따른 예측값(몸무게)가 되는 것이다. 이 식이 선형 회귀라고 불리는 이유는 종속변수가 독립변수에 대해 선형 함수(1차 함수)의 관계가 있을 것이라고 가정하기 때문이다.
- $x$는 독립변수 이외에 입력변수, 예측 변수, 독립 변수 등으로 불린다.
- $y$는 종속변수 이외에 응답변수라고도 불린다.
- $n$은 특성의 수로 독립변수의 종류를 뜻한다.(데이터의 개수와는 다른 의미이다.)
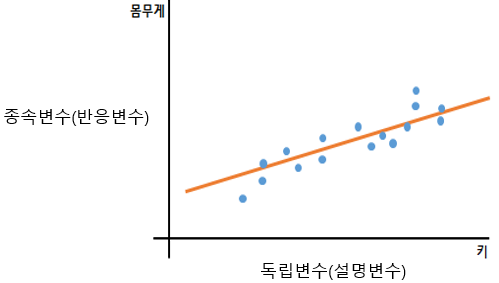
선형회귀모델에서는 몇 가지 가정을 한다. 모든 예측모델이 그렇듯이 모든 경우의 수를 전부 적용하지 못하기 때문에 몇 가지 가정을 두고 예측을 실시한다. 선형회귀모델에서의 가정은 다음과 같다.
- 약한 외생성 : 독립변수 $x$가 확률변수가 아니라 고정된 값으로 취급한다는 것이다. 독립변수에는 에러가 없다는 것을 의미하고 측정 오차로 인해 오염되지 않았음을 가정하는 것과 같다.
(현실적이진 않다.) - 선형성 : 종속변수가 독립변수와 각 계수들의 선형 조합으로 표현이 가능함을 의미한다.
- 상수 분산 : 서로 다른 독립변수들의 오차가 독립변수와 무관하게 항상 같은 분산을 가지는 것을 의미한다.
- 오차의 독립성 : 독립변수의 오차가 서로 무관함을 가정한다는 의미이다.
선형 회귀에도 다양한 종류가 있지만, 크게 ‘단순 선형’과 ‘다중 선형’으로 나뉜다.
단순 선형 회귀
위에 언급한 ‘키와 몸무게’의 관계가 바로 단순선형회귀이다. 한 개의 스칼라 독립변수(키)와 한 개의 스칼라 종속변수(몸무게)의 관계를 말한다. 흔히 알고 있는 1차 함수의 직선이 ‘회귀선(Reagression Line)’이라고 부르고 다른 말로는 ‘단순선형회귀모델’이라고 부른다. 따라서 위에 일반 식에서 단순 선형 회귀는 다음과 같아진다.
\[y = \theta_1\cdot x + \theta_0\]위에서 $n$을 독립변수의 종류라고 표현을 했는데, 단순선형회귀모델에서는 독립변수의 종류가 1개 뿐인 회귀모델이다. 그리고 $n=0$인 $x_0$를 표시하지 않았는데, 이것은 단순히 일반화로 표현하기 위해 표시를 했을 뿐, 실제로는 $x_0=1$이기에 생략을 할 수 있다.
다중 선형 회귀(Multiple Linear Regression)
이름에서도 알 수 있듯이 독립변수가 2개 이상인 것을 ‘다중선형회귀’라고 한다. 보통 실제 세상에는 단순선형 보다는 대부분이 다중선형의 관계를 띄는 경우가 대부분이다. 이 모형에 포함되는 독립변수들을 공변량이라고 하며 각 계수들을 편회귀 계수라고 칭한다.
- 각각의 독립변수가 종속변수에 얼마나 영향을 미치는지 파악할 수 있다
| 방문객(명) | 서비스(점수) | 가격(점수) | 접근성(점수) | 인테리어(점수) | 추천수(개수) |
|---|---|---|---|---|---|
| 5071 | 83 | 50 | 70 | 50 | 70 |
| 1030 | 93 | 10 | 20 | 50 | 100 |
| 7506 | 78 | 71 | 81 | 66 | 12 |
| 5000 | 69 | 56 | 70 | 36 | 72 |
| 1200 | 56 | 55 | 97 | 12 | 120 |
| $\cdot\cdot\cdot$ | $\cdot\cdot\cdot$ | $\cdot\cdot\cdot$ | $\cdot\cdot\cdot$ | $\cdot\cdot\cdot$ | $\cdot\cdot\cdot$ |
위 데이터를 토대로 만든 다중선형회귀 모델은 다음과 같다.
데이터를 이용하여 해당 모델을 예측하여 각 독립변수들에 대한 계수들의 수치를 알면 방문객 수에 가장 많은 영향을 주는 요소가 무엇인지 알 수 있다. 이러한 상관관계 분석을 하는데 있어서 매우 유용한 기법인 것 같다!
실습
Pytorch에는 선형회귀를 쉽고 빠르게 할 수 있도록 모듈을 제공해준다. 밑바닥부터 코딩하기 전에 이미 제공하고 있는 모듈을 이용하여 실습을 진행해보자.
주위에 있던 친구들에게서 데이터를 수집했다. 4명 정도에게서 얻은 데이터는 다음과 같다.
| Index | 몸무게(kg) | 키(cm) |
|---|---|---|
| A | 72 | 174 |
| B | 76 | 180 |
| C | 65 | 169 |
| D | 171 | 68 |
위 데이터를 이용하면 아래의 $\theta$값을 구할 수 있다.
1차 함수
선형회귀모델에서 손실함수를 최소화하는 $\theta$값을 구하는 방법인 ‘정규방정식’이 있다. 하지만 이 방정식을 이용하기 전에 간단하게 1차함수를 구하는 방법으로 $\theta$값을 구해보자. 두 점의 좌표를 알고 있을 때 직선을 구하는 방정식을 이용하는 방법인데, 매우 정확하지 않은 방법이기 떄문에 그냥 참고만 하도록 하자.
먼저 $\frac{\partial y}{\partial x}$는 두 점의 기울기를 뜻하고, 아래와 같이 구할 수 있다.
기울기를 구했으면 1차 함수에서 모르는 값은 $y_0$값 하나 뿐이다. $y_0$값도 간단하게 계산하면 다음과 같다.
\[y_1 = 0.6666x_1 + y_0\]$y_0$값을 제외한 모든 항을 이항하여 1차 방정식을 만들어준다.
이렇게 처음 식 $y = \theta_1x + \theta_0$에서 각각의 계수를 모두 구했다.
Pytorch 코드 실습
Pytorch에서 제공하는 선형회귀함수를 호출하고 위에서 구한 $\theta_0$와 $\theta_1$을 대입하여 선형회귀모델을 생성해보자. 이때 사용하는 모듈은 torch.nn.Linear()이다.
import torch.nn as nn
simple_regression = nn.Linear(1, 1, bias=True) # 인자 : x의 크기, y의 크기, y절편 유무
>>> print(simple_regression)
# Linear(in_features=1, out_features=1, bias=True)
init_weight = simple_regression.weight
init_bias = simple_regression.bias
>>> print(init_weight)
# Parameter containing:
# tensor([[-0.4460]], requires_grad=True)
>>> print(init_bias)
# Parameter containing:
# tensor([-0.0001], requires_grad=True)
>>> print(init_weight.size())
>>> print(init_bias.size())
# torch.Size([1, 1])
# torch.Size([1])
위 코드에서 init_weight와 bias는 각각 $\theta_1$와 $\theta_0$을 뜻한다. 그리고 초기값은 kaiming_uniform을 통해 랜덤으로 초기화된다. 따라서 우리가 찾은 값으로 대체를 해줘야한다.
my_weight = torch.tensor([0.6666], dtype=torch.float).reshape_as(init_weight) # init_weight와 같은 size로 변환
my_bias = torch.tensor([-44], dtype=torch.float).reshape_as(init_bias) # init_bias와 같은 size로 변환
new_weight = nn.Parameter(my_weight)
new_bias = nn.Parameter(my_bias)
simple_regression.weight = new_weight
simple_regression.bias = new_bias
>>> print(simple_regression.weight)
>>> print(simple_regression.bias)
# Parameter containing:
# tensor([[0.6666]], requires_grad=True)
# Parameter containing:
# tensor([-44.], requires_grad=True)
위 코드에서 new_weight와 new_bias을 nn.Parameter()로 감싸주었는데, 그 이유는 nn.Linear()의 Variables의 class가 Parameter이기 때문이다.
>>> type(simple_regression.weight)
# torch.nn.parameter.Parameter
자, 우리가 원하던 선형회귀모델을 얻었다. 실제 결과와 비슷하게 나오는지 확인을 해보자.
cm = [174, 180, 169, 171]
kg = [ 72, 76, 65, 68]
data_x = torch.tensor(cm, dtype=torch.float, requires_grad=False).reshape(len(cm), 1)
data_y = torch.tensor(kg, dtype=torch.float, requires_grad=False).reshape(len(cm), 1)
with torch.no_grad():
kg_prediction = simple_regression(data_x)
>>> print(kg_prediction.reshape(1,-1))
>>> print(data_y.reshape(1,-1))
# tensor([[71.9884, 75.9880, 68.6554, 69.9886]])
# tensor([[72., 76., 65., 68.]])
실제 값과 얼추 비슷한 예측값이 나왔다. 물론 $\theta_1$값이 근사값이라 오차가 많이 날 수 있는데, $\theta_1$값이 수렴할수록 더 정확한 결과가 나온다.
정규방정식
위에서는 두 점의 좌표를 알 때 직선의 방정식을 구하는 방법으로 $\theta$값을 구했다. 하지만 위와 같은 방법은 두 점의 좌표를 알 때 구하는 방법이지, 노이즈가 포함되어 있는 수많은 데이터에 맞는 직선을 찾기 위해서는 예측한 직선과 데이터들 사이의 오차가 최소가 되는 $\theta$값을 찾아야 한다. 즉, 손실함수를 최소화하는 $\theta$값을 찾아야하는데, 그것이 바로 정규방정식이다. 정규방정식을 구하기 전에 먼저 벡터 형태의 선형회구모델의 예측식을 구하면 다음과 같다.
\[\hat{y} = h_\theta(\text{x}) = \theta^T \cdot \text{x}\]- $\theta$는 $\theta_0$에서 $\theta_n$까지의 특성 가중치를 포함하는 파라미터 벡터
- $\text{x}$는 $x_0$에서 $x_n$까지 담고 있는 샘플의 특성벡터이다.($x_0$는 항상 1)
- $h_\theta$는 모델 파라미터 $\theta$를 사용한 가설 함수이다.
그러면 비용함수는 어떻게 구하는 것일까? 선형회귀모델에서 가장 많이 사용되는 성능 측정 지표는 평균 제곱근 오차(RMSE) 이다. 이 지표에 대한 구체적인 내용은 다른 포스터에서 다루기로 하고, 여기서는 단지 $\theta$를 구하기 위한 하나의 방법이라고만 알고 넘어가기로 하자. 하지만 실제로는 RMSE보다 평균 제곱 오차(MSE) 더 선호한다. 그 이유는 같은 결과를 내면서도 더 간단하게 계산할 수 있기 때문이다. MSE의 식은 다음과 같다.
\[\text{MSE}(X,h_\theta) = \frac{1}{m}\sum_{i=1}^m(\theta^T\cdot \text{x}^{(i)}-y^{(i)})^2 = \text{MSE}(\theta)\]이 식을 지지고 볶고 미분하면 손실함수를 최소화하는 $\theta$값을 구하는 정규방정식으로 변한다.
(손실함수$J(\theta)$를 미분했을 때 0이 되도록 하는 $\theta$를 찾는 것이 기본 개념이다.)
- $\hat{\theta}$은 손실함수를 최소로 하는 $\theta$값
- y는 $y^{(1)}$부터 $y^{(m)}$까지 포함하는 종속변수 벡터
위의 식을 코드로 계산을 하면 다음과 같다.
\[\begin{aligned} & (1)\qquad (\text{X}^T\cdot \text{X})^{-1} \\ & (2)\qquad (1)\cdot \text{X}^T \\ & (3)\qquad (2)\cdot y\\ \end{aligned}\]Pytorch 코드 실습
def dot(a,b): # dot : a와 b의 내적
return torch.matmul(a,b)
cm = [174, 180, 169, 171] # x
kg = [ 72, 76, 65, 68] # y
data_x = torch.tensor(cm, dtype=torch.float, requires_grad=False).reshape(len(cm), 1)
data_y = torch.tensor(kg, dtype=torch.float, requires_grad=False).reshape(len(cm), 1)
X = torch.cat((torch.ones_like(data_x), data_x), 1) # torch.cat(a,b) : 두 행렬 합치기
y = data_y
dot1 = torch.inverse(dot(X.T, X)) # (1) torch.inverse() : 역행렬 #
dot2 = dot(dot1, X.T) # (2)
dot3 = dot(dot2, y) # (3)
>>> print(dot3)
# tensor([[-99.4848],
# [ 0.9784]])
선형회귀모델을 최소로 하는 $\theta$를 구하기 위해 ‘두 좌표로 구하는 방식’과 ‘정규방정식으로 구하는 방식’을 사용했다. ‘두 좌표로 구하는 방식’으로 구할 때와 사뭇 다른 결과가 나왔지만, 매우 당연한 결과이다. 두 점으로 만든 직선이 모든 데이터에 대해 적용되었다고 볼 수 없기 때문이다. ‘정규방정식’ 또한 현재는 모집단이 매우 작기 때문에 일반화를 하기에는 많이 부족하다.
의문점
사실 ‘정규방정식’으로 구하는 과정에서 필자를 매우 혼란스럽게 만든 부분이 있다. 위 코드에서도 언급이 되었는데, 다시 한 번 그 부분만 자세히 보면 다음과 같다.
X = torch.cat((torch.ones_like(data_x), data_x), 1) # torch.cat(a,b) : 두 행렬 합치기
>>> print(X)
# tensor([[ 1., 174.],
# [ 1., 180.],
# [ 1., 169.],
# [ 1., 171.]])
‘정규방정식’에서 사용되는 X를 만드는 코드이다. 여기서 torch.ones_like(data_x)를 사용했는데, 1로 구성된 더미변수이다.
>>> torch.ones_like(data_x)
# tensor([[1.],
# [1.],
# [1.],
# [1.]])
책에서도 그렇고 모든 블로그에서도 너무 당연한 것 처럼 이 부분에 대해 언급하는 사람이 없어서 굉장히 당황스러웠다. 필자는 머리가 매우 좋지 않아서 왜 더미변수를 추가하는지 이해를 못 했기 때문이다. 심지어 이걸 알아내는데 이틀이나 걸렸다. 이틀을 고민했는데 3일차에 자고 일어나니 띵! 하면서 득도를 해서 어이가 없었다. (필자와 마찬가지로 대부분의 블로거들이 ‘핸즈온 머신러닝’을 참고하는 것 같다. 그 책에서 이 부분이 나오기 때문에….)
단순선형회귀에는 독립변수$x$가 1종류 뿐이기 때문에 1차 함수와 같은 모양이다.
하지만! 여기서 필자가 놓치고 간 부분이 $\theta_0$ 부분이있다. 위 식은 사실 아래와 같은 식으로 표현된다.
$x_0$도 식에 있어야 하지만, $\theta_0$값이 편향이기 때문에 $x_0 =1$을 가정한다. 그래서 사실상 $\theta_0$는 $x_0$에 대한 계수로 볼 수 있고, 이는 곧 독립변수가 2종류가 된다는 뜻이다.(그렇다고 다중 선형회귀라는 뜻은 아니다. 그냥 그런 의미로~) 하지만 모두 예상한대로 이 값은 1이기 때문에 더미변수로 X변수에 추가를 해 주었고, ‘정규방정식’에 의해 2개의 결과나 나온 것을 알 수 있다. 이 사실을 몰랐던 필자는 처음에 계속 $\theta_1$의 결과만 나와서 혼란스러웠다. 굉장히 초보?스러운 질문인 것 같아서 부끄럽지만 혹시나 필자와 같은 고민을 하는 독자가 있을 것 같아서 언급을 했다.
지금까지 선형회귀와 실제로 데이터를 통해 계수들을 찾는 방법에 대해 알아보았다. 사실 위와 같은 방법들은 굳이 pytorch가 아니라 numpy, scipy 등을 이용해도 충분히 구할 수 있는 방법이다. 이 포스터는 목적은 선형회귀를 이해하는 것이기 때문에 다음 포스터에서 Pytorch만의 기능을 이용하여 선형회귀를 구해보도록 하자.